 (source)
(source)
|
Lawrence Hargrave
(29 Jan 1850 - 6 Jul 1915)
Australian aeronaut and inventor made important studies of wing surfaces for flying-machines, and invented the box kite.
|
Lawrence Hargrave
Flying-Machine Model and Kite Inventions
from Progress in Flying Machines (1894)
[p.218] If there be one man, more than another, who deserves to succeed in flying through the air. that man is Mr. Laurence Hargrave, of Sydney, New South Wales. He has now constructed with his own hands no less than 18 flying machines of increasing size, all of which fly, and as a result of his many experiments (of which an account is about to be given) he now says, in a private letter to the writer, that: “I know that success is dead sure to come.”
M. Hargrave takes out no patents for any of his aerial inventions, and he publishes from time to time full accounts of them, in order that a mutual interchange of ideas may take place with other inventors working in the same field, so as to expedite joint progress. He says: “Workers must root out the idea that by keeping the results of their labors to themselves a fortune will be assured to them. Patent fees are so much wasted money. The flying machine of the future will not be born fully fledged and capable of a flight for 1,000 miles or so. Like everything else it must be evolved gradually. The first difficulty is to get a thing that will fly at all. When this is made, a full description should be published as an aid to others. Excellence of design and workmanship will always defy competition.”
M. Hargrave is probably correct in his reasoning; for the history of all new methods of transportation teaches that the original inventor seldom receives pecuniary reward for the contrivance which is the first to succeed, but nevertheless he is certainly broadly liberal in giving to [p.219] the world gratuitously the results of his constant studies and labors. He uses exceeding care in determining the different elements which compose the flight of his models. He has carefully registered the sizes of all the parts, the power consumed in each performance, and the length of the flight, together with its trajectory. He states that he has always kept his work in such shape that it could be taken up and continued by any person at any time; so that a stranger, if an expert, could come into his shop, study his notes and drawings, pick up his tools and continue his work, and thus no portion of it would be lost.
M. Hargrave reports regularly the progress of his work to the Royal Society of New South Wales, of which he is a member. Thus far 13 such papers have been published, the latest having been read June 7, 1893.
He first devoted his attention to the motions performed by the propelling surfaces of birds and fishes, the waves which these created in the fluids on which they acted, and the counteraction of these waves upon the forms of the propelling, surfaces themselves. The first paper, therefore, presented in August, 1884, was on the Trochoided plane, which M. Hargrave defines as “a flat surface, the center of which moves at a uniform speed in a circle, the plane being kept normal to the surface of a trochoidal wave, having a period equal to the time occupied by the center of the plane in completing one revolution.” This was illustrated by working models, and the motions of wings and of fishes in swimming were artificially reproduced.
Starting from these data, M. Hargrave next experimented with nearly 50 models intended to reproduce horizontal flight, and in exhibiting some of these and reading his second paper, June, 1885, he said: “If the motion is not that used by birds, it is at all events very like it, and its acceptance or rejection as a scientific truth is of no further interest, as it only remains for practical mechanics to step in and adjust the details to suit the material and the motive power which they may think best for the purpose they have in view; or, in other words, that the solution of the problem of just how a bird flies is of very trifling importance from a practical standpoint, as compared with the judicious variations of the parts of the machine that will have to be made before any return can he expected for money invested in such undertakings.”
Some of these models seem to have been driven by clock-work, and the motions were those of the “trochoided planes,” as applied to flapping wings; then selecting the best of these models, and making their mean dimensions [p.220] a standard from which to take a fresh departure, M. Hargrave next built a series of experimental flying machines, actuated by india-rubber in tension.
The French experimenters, as we have seen, have preferred to use rubber in torsion in order to diminish the strains upon the central spine or backbone of the model, but they thus obtained less energy per pound of weight than if they had used it in tension. M. Hargrave stretched the rubber so that its elongation was multiplied by pulley-tackle, and that, as the rubber contracted, its center of gravity moved forward, thus advancing the center of gravity of the entire machine, and consequently diminishing the angle of flight as the force of the rubber decreased.
No less than 10 different flying machines of various types were thus built and experimented with, all moved by rubber in tension. In the first models the cord proceeding from the rubber was wound around a cylindrical drum on the crank-shaft, but owing to the variable resistance natural to a crank-shaft, it was found better to replace the cylindrical drum by a flat winder, so adjusted on the shall that the moment of the cord varied with the resistance of the crank, and thus communicated a more uniform movement to the wings.
Seven of these machines seem to have been propelled by flapping wings—i.e., “trochoided planes”—but in order that a comparison might be made, three varieties of models were made with screw propulsion—namely, with double and with single screws in the bow, and with a single screw in the stern, which latter was concluded to be the most practicable and serviceable form.
From these experiments M. Hargrave concluded that the screw and the flapping wings are about equally effective as instruments of propulsion, although he rather prefers the latter, as the wings possess several marked advantages. Any currents, he says, initiated during the upstroke are utilized in giving increased efficiency to the down-stroke, if the machine has not progressed far enough to be acting upon entirely undisturbed air'. Moreover, when steam-engines come to be used, there will be only one cylinder needed for both wings, there will be no conversion of reciprocating into rotary motion, and no variable listing moment to be counteracted, while, finally, there is less liability that wings shall be damaged in alighting than screw blades.
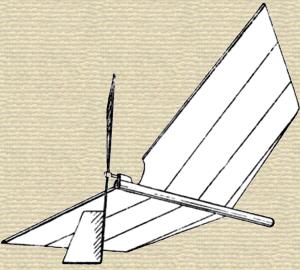
Fig. 76 shows the last one (1889) of the india-rubber driven machines described by M. Hargrave. He calls it the “48 band-screw.” The screw is at the stern, and the machine weighs exactly 2 lbs. Its sustaining area is 14.51 sq. ft. (7.26 sq. ft. per pound), and it flew 120 lineal feet [p.221] with the expenditure of 196 foot-pounds of energy, while the preceding machine, weighing 2.09 lbs., with flapping wings, had flown 270 ft. with 470 foot-pounds, thus showing respectively 0.61 and 0.57 lineal feet flown per foot-pounds of power.
The framework of these machines was of pine, the larger piece (main spine) being a hollow box-girder, to secure strength and lightness. The sustaining surfaces were of paper, pasted on, and after the gum was dry rendered as tight as a drum by blowing a light spray of water over the paper and allowing it to dry. Thus with small, light, simple, and inexpensive models many experiments were made, and great advance realized in the distance flown over any previous experiments of others.
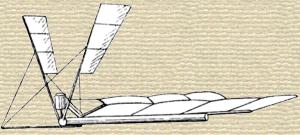
Having progressed thus far with india-rubber as a motive power, and gathered most valuable data and experience; as to the best arrangement and proportion of parts, the equipoise and the power required, M. Hargrave next undertook the construction of a flying machine actuated by compressed air, and, in 1890, he produced the machine illustrated by fig. 77, which he calls his “ No. 10, 40.5 oz. compressed air,” and which marked a very considerable advance in design by a great simplification of the propelling arrangement.
In presenting it to the Royal Society, June 4, 1890, M. Hargrave said;
The principle embodied in this experiment is that of Borelli, [p.222] published in 1680, and it doubtless has had many stanch advocates in later times; but the writer maintains that this is the first practical demonstration that a machine can and does fly by the simple (vertical) flapping of wings; the feathering, tilting, twisting, trochoiding, or whatever it may be called, being solely effected by torsional stress on the wing arms.
The combination of Borelli's views with the results of work recorded in your proceedings (Royal Society) has swept away such a mass of tackle from the machine that its construction becomes a ridiculously simple matter. The engine of the model, of course, retains its precedence as the most important part, and by continuous effort the number of pieces and the difficulties of construction have been so reduced that it is possible to make them by the gross at a cost that cannot exceed five shillings each ($1.25). For instance, the cylinder, usually the most expensive portion of an engine, can be produced with the ease and celerity of a tin can. ...
It might be said that this flying machine is not on the principle enunciated by Borelli, because the wings are not continuous from their tip to the body. But this arrangement is only a device to enable the wing tips to act on the required quantity of air with less spread ; it may possibly be one of those variations which make all the difference between success and failure. These wings are also distinctly double-acting, and it is not quite clear that birds' wings thrust during the up-stroke; but, as previously stated, the question as to the exact movement of a. bird's wing is merely straw-splitting, when we have a mechanism that actually flies and is manifestly imperfect in its present mechanical details.
This machine flew 368 ft., with the expenditure (as corrected by M. Hargrave) of 870 foot-pounds of energy. It weighed 2.53 lbs., and the sustaining body plane measured 14.78 sq. ft., while the two wings measured 1.50 sq. ft. in area, making a total of 16.28 sq. ft., or, say, 6.43 sq. ft. per pound.
London Engineering, in its issue of December 26, 1890, gives the following description of the machine:
The compressed air is stored in a tube which forms the backbone of the whole construction. This tube is 2 in. in diameter, 48¼ in. long, and has a capacity of 144.6 cub. in. Its weight is 19.5 oz., and the working pressure is 230 lbs. per square inch. The engine cylinder has a diameter of 1½ in. and a stroke of 1¼ in., while the total weight of the engine is only 6½ oz. The piston-rod is made fast to the end of the backbone, and the cylinder moves up and down over the piston. Two links connect the cylinder to the Canadian red pine rods which carry the wings. The air is admitted to the cylinder and exhausted by means of a valve worked by tappets. The period of admission continues through the entire stroke. The cylinder and receiver ends are pressed, and the piston is made of vulcanite, with a leather cup ring for packing.
[p.223] The wings are made of paper, and have no canting or feathering motion other than that due to the springing of the material of which they are made. The weight of the wings is 3 oz. To find how much the wings deflected, one was held by the butt and a weight of 7½ oz. was put on the membrane 24 in. from the fixed point, and 1-5/8 in. abaft the wing arm. The deflection produced, due to torsional stress, was 3½° . By moving the weight half way across the wing it was twisted 8¼°. The area of the body is 2.128 sq in.; the area of the wings 216 sq. in., and the total area 2.344 sq. in.
When first made, the machine had its center of gravity so placed that the percentage of area in advance of it was 30 per cent, of the whole area, but continued disaster caused its reduction to 23.3 per cent. In a dead calm the machine flew 368 ft. horizontally.
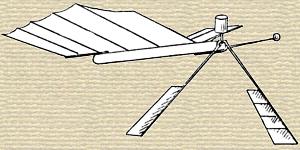
It will be noted that the engine is a marvel of simplicity and lightness. Its cylinder is made like a common tin can, the cylinder covers are cut from sheet tin and pressed into shape in a vice, the piston and junk-ring are made of vulcanite, and the cup leather packing does away with the necessity for the cylinder being either round or parallel.
Beside the engine, a marked advance consisted in securing the torsion of the wings through no special mechanism, as formerly, but simply by the elasticity of the material composing them. This throws a new light upon the part performed in the flight of birds by the elasticity of their feathers, and promises great simplicity and efficiency in the future designing of artificial wings.
By looking at the figure, a bowsprit will be noticed. This was a so-called safety stick, which was added to break the fall of the machine when alighting, and it has proved quite successful in accomplishing that object.
A noticeable feature of this and subsequent machines exhibited by M. Hargrave consists in the extraordinary length of its supporting body plane. The same surface [p.224] would carry a far greater load if it were driven broadside instead of lengthwise; but M. Hargrave explains that the plane was purposely so designed in order to insure longitudinal stability. This quality might also be secured by placing a tail far in the rear of a narrow supporting plane, as practiced by Penaud and others. He states, moreover, that the plane is rendered more effective per unit of surface by being cut away in the middle portion, or by being formed in two parts, separated by a gap.
As regards the lateral equilibrium, he seems to have met with but little difficulty ; a slight diedral angle of the two halves of the body plane with each other providing the necessary stability, and preventing any swerving, so long as the center of gravity was at all below the center of effort; but he had great trouble in working out the longitudinal stability. This he did upon the “cut and try” principle—a method doubtless the most thorough, the surest, and the most convincing, but also the most tedious. He found that the direction up or down of the machines in flight was entirely due to the distance of the center of gravity from the forward edge of the body plane, and therefore to the coincidence or otherwise of the center of gravity with the center of pressure. He measured the percentage of area in advance of the center of gravity in his three most successful machines, and found it respectively 19, 3.20 and 23.3 per cent, of the length of the plane, while subsequently he came to the general conclusion that the true position for the center of gravity for a continuous rectangular surface is situated between 0.25 and 0.2 of the length from the forward end, these positions being arrived at “by experience gained by repeated wrecks when groping in comparative darkness.”
This independent working out of a complex question well illustrates the perseverance and ingenuity of this experimenter. At this juncture, however, he would have been saved much groping, time, and annoyance had he been aware of the formula of Joessël for determining the center of pressure:
C = (0.2 + 0.3 sin. a) L,
in which C is the distance from the forward edge of a rectangular plane to its center of pressure, when inclined at the angle of incidence a with the course, and L is the length of the plane along the line of motion.
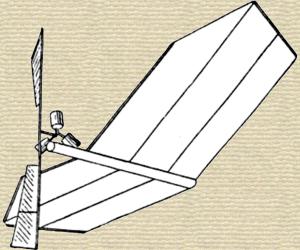
In the same year (1890) M. Hargrave built another flying machine, actuated by compressed air and propelled by beating wings. This is shown by fig. 78. It was of the increased weight of 4.63 lbs., with sustaining body plane of different shape, measuring 29.63 sq. ft., or in the [p.225] proportion of 6.40 sq. ft. per pound. It flew 343 ft., with an expenditure of 789 foot-pounds of energy, and therefore showed better results than the previous machine (No. 10), inasmuch as more pounds were transported on the air approximately the same distance, with a somewhat smaller expenditure of energy.
Having apparently found some advantage by shortening the body plane, M. Hargrave next built his flying machine No. 13, which s shown in fig. 79, with a body plane still shorter, and he provided it with a two-bladed aerial screw, set in the bow and actuated by a three-cylinder compressed-air engine of the Brotherhood type. This drove it 128 ft. in eight seconds, with an expenditure of 143 foot-pounds of energy. The apparatus weighed 46.86 oz. (2.93 lbs.), and exposed 2,952 sq. in. or 20.5 ft. of floating surface, being in the ratio of 7.00 sq. ft. per pound.
This is the first time (paper 10, July 1, 1891) that M. Hargrave gives us the time of flight of his machines, so that we may calculate the number of pounds of weight transported in ratio to the horse power. He says:
The time of flight is taken with a sandglass which has a loop of string at each end of it. The loop at the sand end is put round the right wrist, and the other loop is held between the right thumb and the receiver, so that the glass is turned the moment that the machine is let go. On the machine taking the ground the glass is put horizontal, and the sand which has fallen is timed at leisure. This seems an obvious enough method of finding the speed, but a practical way to do it was not devised previously.
This showed for No. 13 machine a speed of 10.34 miles per hour, which is about what we should have expected from the large proportional surface, it being about in the ratio of the slowest flying birds. This low speed M. Hargrave [p.226] adopts on purpose, the better to observe the motions of the machines and to save breakage, and he adds quaintly that he sees no objection to this course, so long as the atmosphere is not crowded with flying machines. As No. 13 machine (fig. 79) is reported as having expended 143 foot-pounds in eight seconds, we have:
Power = 143 ÷ 8 = 18 foot-pounds per second,
nearly, and, as it weighed (as reported) 2.93 lbs., we have for the weight sustained per horse power;
2.93 × 550 ÷ 18 = 89.53 lbs. per horse power;
while it will be recollected that M. Tatin sustained 110 lbs. per horse power and that M. Phillips in his recent (1893) experiments floated 72 lbs. per horse power. We will see by the analysis of subsequent performances that M. Hargrave did not obtain quite as good results with subsequent flying machines.
He next built his No. 14 flying machine, with much the same shape of body surface, but propelled by beating wings instead of a screw. It weighed 3.69 lbs. and exposed 22.84 sq. ft. of surface, being in the proportion of 6.19 sq. ft. per pound. It flew 312 ft. in 19 seconds, with an expenditure of 509 foot-pounds, and thus we have;
Power = 509 ÷ 19 = 26.79 foot-pounds per second,
and for the weight floated per horse power;
3.69 × 550 ÷ 26.79 = 75.75 lbs. per horse power.
This apparatus (No. 14) M. Hargrave has generously offered to present to some American institution which will take proper care of it, believing it to be one in which “the increased skill in construction acquired by practice is thought to have resulted in an apparatus that, for its weight, it will be hard to excel.” He says in his paper to the Royal Society:
It may be said that it is a waste of time to make machines of such small capabilities, and that no practical good can come of them. But we must not try too much at first; we must remember that all our inventions are but developments of crude ideas; that a commercially successful result in a practically unexplored field cannot possibly be got without an enormous amount of unremunerative work. It is the piled-up and recorded experience of many busy brains that has produced the luxurious travelling conveniences of to-day, which in no way astonish us, and there is no good reason for supposing that we shall always be content to keep on the agitated surface of the sea and air, when it is possible to travel in a superior plane, unimpeded by frictional disturbances.
[p.227] No. 16 was another compressed-air flying machine with beating wings and somewhat differently shaped body plane. It weighed 4.66 lbs., spread 26.06 sq. ft. of surface, and flew 343 ft. in 23 seconds, with an expenditure of 742 foot-pounds. The power was therefore;
Power = 742 ÷ 23 = 32.26 foot-pounds per second,
and the weight floated per horse power:
4.66 × 550 ÷ 32.26 = 79.45 lbs. per horse power.
Several forms of body plane seem to have been tested in this machine and no less than 12 trials were recorded, trial No. 10 being the successful one, from which the above data have been taken.
Having now constructed 10 flying machines of different types and proportions actuated by india-rubber in tension, and six actuated by compressed air, of increasing size and weight, M. Hargrave then turned his attention to producing a steam motor which should equal in lightness and surpass in power the best compressed-air motors thus far constructed by him, and which should furnish driving power for a longer time.
But first he endeavored to work out an idea which he seems to have entertained for some years, of testing an explosion motor. His engine No. 15 consisted of a turbine to be worked by the gases resulting from the explosion of a mixture of nitrate of ammonia, charcoal, and sulphur; but a considerable expenditure of time only resulted in a failure.
He also experimented upon a method of utilizing sea [p.228] waves in propelling vessels, which he believes to be the germ of the solution of the soaring problem, and he succeeded in securing such automatic action that a 12½ lb. mode advanced in the wind's eye at five-eighths of a mile per hour.
He also made some experiments upon pure aluminium, but found that it presented no advantages for flying-machine construction.
No. 17 flying machine of M. Hargrave is described in his twelfth communication to the Royal Society of New South Wales, read August 3, 1892. The total weight of the apparatus is 64.5 oz., or 4.03 lbs., including 12¾ oz. for the strut and body plane, so that the engine and boiler, including 5 oz. for spirit fuel and water, weighs 3.25 lbs., and develops 0.169 horse power, or at the rate of 1 H. P. per 19.2 lbs.—a very remarkable achievement.
The boiler is of the “Serpollet” type, made of 12 lineal feet of ¼ in. copper tubing (steel pipe could not be got in Sydney), in the form of a double-stranded coil, encased in asbestos, and placed just over the backbone of the apparatus. The fuel is methylated spirits of wine, drawn from a tank placed above the boiler, vaporized, mixed with air and spurted into the furnace. As much as 6.9 cub. in. of water have been evaporated by 1.7 cub. in. of spirit in 80 seconds, making 182 double vibrations of the propelling wings, say, 2.35 per second, and developing 0.169 horse power.
It was estimated that if the apparatus were loaded with 10 oz. more of spirit and water, and thus made to weigh the same as the compressed-air machine No. 12, which flew 343 ft., then the steam apparatus No. 17 would possess a sufficient store of energy to fly 1,640 yds., or nearly 1 mile.
But M. Hargrave has done still better, for in March, 1893, he prepared a paper, which was presented to the Conference on Aerial Navigation at Chicago, August 2, 1893, in which he gave data concerning his No. 18 flying machine. This apparatus is also driven by a steam-engine which weighs, with 21 oz. of fuel and water, an aggregate of 7 lbs , and indicates 0.653 horse power, or at the rate of 10.7 lbs. per horse power; so that, roughly speaking, the weight of the motor has been doubled, and the power has been increased fourfold.
Four boilers were constructed. The final one was made of 21 lineal feet of ¼ in. copper pipe, with an internal diameter of 0.18 in., and arranged in three concentric vertical coils whose diameters were 1.6 in., 2.6 in., and 3.6 in. respectively. It weighed 37 oz., but it is now known “that a coil of equal capacity can be made weighing [p.229] only 8 oz., and still excessively strong.” The cylinder is 2 in. diameter, with a stroke of 2.52 in. The feed-pump ram is 0.266 in. diameter, and the piston valves 0.3 in. diameter. On one occasion this motor evaporated 14.7 cub. in. of water with 4.13 cub. in. of spirit in 40 seconds. During a portion of the time it was working at a speed of 171 double vibrations per minute.
M. Hargrave gives no data concerning the flight of his last two (steam) machines. He states that 11 different burners have been tried, and that the flame striking the water boiler first has a tendency to vary the supply of heat to the spirit holder. From this it is inferred that he is struggling with the same difficulties already encountered by Stringfellow, by Moy, and by Maxim in regulating and keeping alight spirit burners when the apparatus gets under forward head-way; but this difficulty, while a serious one, will doubtless be eventually overcome by persistent experiment, and we may then expect flights of astonishing lengths.
Seeing now his way to an adequate motor and to extensive flights in the near future, M. Hargrave recently turned his attention to experiments upon curved surfaces, and to the seeking for a better disposition of the sustaining surfaces or body planes. He had described the eccentricities of a curved strip in the form of a segment of a hollow cylinder, when exposed to the wind, in his paper No. 12 to the Royal Society of New South Wales, read August 3, 1892, and he describes some of his experiments with “cellular kites,” in his paper read in the Aerial Navigation at Chicago, August 2, 1893.
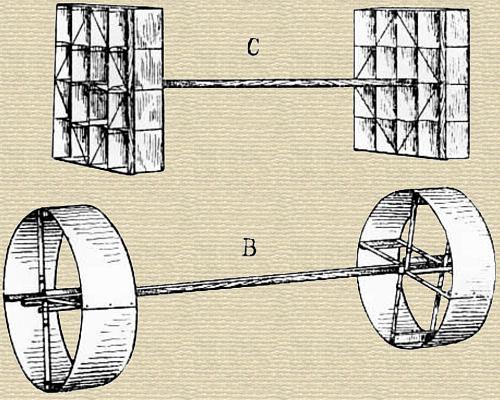
The “cellular kites” constitute quite a new departure, and practically consist of superposed aeroplanes connected together in pairs. B, in fig. 80, shows the simplest form. This consisted of two hollow cylinders of aluminium, each 13 in. diameter by 44 in. deep, mounted 30 in. apart upon a connecting stick, and weighing 14¾ lbs. The kite-string was attached 11 in. back from the forward section, and as a consequence of the angle of incidence thus produced, the apparatus mounted upon the wind. Its particular behavior is not described in the paper. C, in fig. 80, shows a kite with 16 cells, the length of each being 3 in., by a height of 3 in., and a breadth of 3 in. It was made of cardboard, and the two sections were 22 in. apart, the point of attachment of the kite-string being 6½ in. distant from the forward section, while the weight was 10.5 lbs. This seems to indicate that this kite flew at a steeper angle than the preceding, although we should expect the reverse, in consequence of the greater proportion of sustaining surface. M. Hargrave says, “These kites have a fine angle of incidence, so that they correspond with the flying machines they are meant to represent, and differ from the kites of our youth, which we recollect floating at an angle of about 45°, in which position the lift and the drift are about equal. The fine angle makes the lift largely exceed the drift, and brings the kite so that the upper part of the string is nearly vertical.”
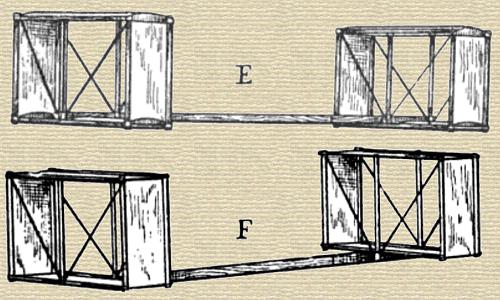
Kites E and F, fig. 81, are of exactly the same size and weight, consisting of one cell, 4 in. long, 10.7 in. broad by 6.25 in. high, constructed of wood and paper, and weighing 3.25 lbs.; the two sections are 21.25 in. apart, and the string is fastened 7.25 in. back of the forward section. The only difference is that kite E has its horizontal (top and bottom) surfaces curved to a radius of 4.5 in., while all the surfaces of kite F are true planes. The result is that when kite E is flown with the convex sides up, it pulls about twice as hard on the string as kite F, so that, as M. Hargrave says; “A flying machine with curved surfaces would be better than one with a flat body plane, if the form could be made with the same weight of material.”
M. Hargrave, in this last paper, figures and describes two other forms of cellular kites with which he has experimented, and points out that the rectangular form of cell is collapsible when one diagonal tie is disconnected, so as to make it easy of transportation. He says; “Theoretically, [p.231] if the kite is perfect in construction and the wind steady, the string could be attached infinitely near the center of the connecting stick, and the kite would fly very near the zenith. It is obvious that any number of kites may be strung together on the same line, and that there is no limit to the weight that may be buoyed up in a breeze by means of light and handy tackle. The next step is clear enough—namely, that a flying machine with acres of surface can be safely got under way, or anchored and hauled to the ground by means of the string of kites.”
He duly gives credit to M. Wenham for suggesting the superposition of planes in 1866, and it is an interesting circumstance to note that at the same Chicago Conference, a paper from M. Wenham was read suggesting a course of experiments with kites, to determine the best arrangement of superposed aeroplanes and the conditions of equipoise.
Such are the labors of M. Hargrave up to the present time. He no longer troubles himself about the general problem of man's eventual success in navigating the air, but he says: “The people of Sydney who can speak of my work without a smile are very scarce; it is doubtless the same with American workers. I know that success is dead sure to come, and therefore do not waste time and words in trying to convince unbelievers.”
[p.233] Instead of this, he constructs machines and reports the results in detail, so that others may repeat his experiments. He says that the record of unsuccessful experiments takes up a considerable portion of his notes, and further, that “there is no use in the mind's conceiving an idea, if the hands are not ready to carry out the work skillfully, in the absence of reliable assistance, and if the design be found faulty, the whole thing should be begun again without trying to use up old machines. The question of intricate workmanship and costliness is being continually battled with ; my constant endeavors are directed to making the machines simple and cheap, so that any one who doubts can verify my work, provided his hands are as skillful as mine, and I am sure that the photographs show clearly that the workmanship is anything but first-rate”
He began with small, cheap models, and has gradually enlarged their size, and obtained flights longer than any heretofore accomplished. It is noticeable that the heavier the model, and the smaller the sustaining area in proportion to the weight, the more successful has been the flight. He may not be the first man to ride at will upon the air, but he deserves to succeed.
- Science Quotes by Lawrence Hargrave.
- 29 Jan - short biography, births, deaths and events on date of Hargrave's birth.




