 (source)
(source)
|
Paul A. M. Dirac
(8 Aug 1902 - 20 Oct 1984)
English theoretical physicist known for his work in quantum mechanics and for his theory of the spinning electron. In 1933 he shared the Nobel Prize for Physics with the Austrian physicist Erwin Schrödinger.
|
Science Quotes by Paul A. M. Dirac (40 quotes)
>> Click for Paul A. M. Dirac Quotes on | Biography | Equation | Mathematics | Physics |
>> Click for Paul A. M. Dirac Quotes on | Biography | Equation | Mathematics | Physics |
[There is] some mathematical quality in Nature, a quality which the casual observer of Nature would not suspect, but which nevertheless plays an important role in Nature’s scheme.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 122.
A good deal of my research in physics has consisted in not setting out to solve some particular problem, but simply examining mathematical quantities of a kind that physicists use and trying to fit them together in an interesting way, regardless of any application that the work may have. It is simply a search for pretty mathematics. It may turn out later to have an application. Then one has good luck. At age 78.
— Paul A. M. Dirac
International Journal of Theoretical Physics (1982), 21, 603. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 110.
A great deal of my work is just playing with equations and seeing what they give.
— Paul A. M. Dirac
Quoted in Frank Wilczek, ',The Dirac Equation'. Proceedings of the Dirac Centennial Symposium (2003), 45.
A theory with mathematical beauty is more likely to be correct than an ugly one that fits some experimental data. God is a mathematician of a very high order, and He used very advanced mathematics in constructing the universe.
— Paul A. M. Dirac
In Scientific American (May 1963). As quoted and cited in The Hutchinson Encyclopedia of Science (1998), 468.
As time goes on, it becomes increasingly evident that the rules which the mathematician finds interesting are the same as those which Nature has chosen.
At age 36.
At age 36.
— Paul A. M. Dirac
"Proceedings of the Royal Society of Edinburgh (1939), 59 122. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 109-110. This quote is also on this web page in a longer version that begins, “Pure mathematics and physics are… ”.
God used beautiful mathematics in creating the world.
— Paul A. M. Dirac
Quoted in Behram Kursunoglu and Eugene Paul Wigner, Paul Adrien Maurice Dirac (1990), Preface, xv.
Hopes are always accompanied by fears, and, in scientific research, the fears are liable to become dominant.
At age 67.
At age 67.
— Paul A. M. Dirac
Eureka (Oct 1969), No.32, 2-4.
I admired Bohr very much. We had long talks together, long talks in which Bohr did practically all the talking.
Recalling his Sep 1926-Feb 1927 stay in Copenhagen.
Recalling his Sep 1926-Feb 1927 stay in Copenhagen.
— Paul A. M. Dirac
In History of Twentieth Century Physics (1977), 109. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 94.
I consider that I understand an equation when I can predict the properties of its solutions, without actually solving it.
— Paul A. M. Dirac
Quoted in F Wilczek, B Devine, Longing for the Harmonies.
I do not see how a man can work on the frontiers of physics and write poetry at the same time. They are in opposition. In science you want to say something that nobody knew before, in words which everyone can understand. In poetry you are bound to say ... something that everyone knows already in words that nobody can understand.
Commenting to him about the poetry J. Robert Oppenheimer wrote.
Commenting to him about the poetry J. Robert Oppenheimer wrote.
— Paul A. M. Dirac
Quoted in Steven George Krantz, Mathematical Apocrypha Redux: More Stories and Anecdotes of Mathematicians (2005), 169
I found the best ideas usually came, not when one was actively striving for them, but when one was in a more relaxed state… I used to take long solitary walks on Sundays, during which I tended to review the current situation in a leisurely way. Such occasions often proved fruitful, even though (or perhaps, because) the primary purpose of the walk was relaxation and not research.
— Paul A. M. Dirac
'Methods in Theoretical Physics', From A Life of Physics: Evening Lectures at the International Centre for Theoretical Physics, Trieste, Italy. A Special Supplement of the IAEA Bulletin (1968), 24.
I learnt to distrust all physical concepts as the basis for a theory. Instead one should put one's trust in a mathematical scheme, even if the scheme does not appear at first sight to be connected with physics. One should concentrate on getting interesting mathematics.
— Paul A. M. Dirac
From a 1977 lecture. Quoted in Pesi Rustom Masani, Norbert Wiener, 1894-1964 (1990), 6.
I think it is a peculiarity of myself that I like to play about with equations, just looking for beautiful mathematical relations which maybe don’t have any physical meaning at all. Sometimes they do.
At age 60.
At age 60.
— Paul A. M. Dirac
"Interview with T. Kuhn (7 May 1963), Niels Bohr Library, American Intitute of Physics, New York. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 109.
I think it is the general rule that the originator of a new idea is not the most suitable person to develop it, because his fears of something going wrong are really too strong…
At age 69.
At age 69.
— Paul A. M. Dirac
The Development of Quantum Theory (1971). In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 111.
In science one tries to tell people, in such a way as to be understood by everyone, something that no one ever knew before. But in poetry, it’s the exact opposite.
— Paul A. M. Dirac
As quoted, without citation, in Robert Jungk and James Cleugh (trans.), Brighter Than a Thousand Suns: A Personal History of the Atomic Scientists (1958), 22. The writing of poetry by Robert Oppenheimer was being remarked upon by Dirac, as he was talking with him.
It is more important to have beauty in one's equations than to have them fit experiment... It seems that if one is working from the point of view of getting beauty in one's equations, and if one has really a sound insight, one is on a sure line of progress. If there is not complete agreement between the results of one's work and experiment, one should not allow oneself to be too discouraged, because the discrepancy may well be due to minor features that are not properly taken into account and that will get cleared up with further developments of the theory.
— Paul A. M. Dirac
In 'The Evolution of the Physicist’s Picture of Nature', Scientific American, May 1963, 208, 47.
Just by studying mathematics we can hope to make a guess at the kind of mathematics that will come into the physics of the future ... If someone can hit on the right lines along which to make this development, it m may lead to a future advance in which people will first discover the equations and then, after examining them, gradually learn how to apply the ... My own belief is that this is a more likely line of progress than trying to guess at physical pictures.
— Paul A. M. Dirac
'The Evolution of the Physicist's Picture of Nature', Scientific American, May 1963, 208, 47. In Steve Adams, Frontiers (2000), 57.
Let us now discuss the extent of the mathematical quality in Nature. According to the mechanistic scheme of physics or to its relativistic modification, one needs for the complete description of the universe not merely a complete system of equations of motion, but also a complete set of initial conditions, and it is only to the former of these that mathematical theories apply. The latter are considered to be not amenable to theoretical treatment and to be determinable only from observation.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 125.
Mathematics is the tool specially suited for dealing with abstract concepts of any kind and there is no limit to its power in this field.
— Paul A. M. Dirac
The Principles of Quantum Mechanics (1930, 1981), Preface, viii.
One might describe the mathematical quality in Nature by saying that the universe is so constituted that mathematics is a useful tool in its description. However, recent advances in physical science show that this statement of the case is too trivial. The connection between mathematics and the description of the universe goes far deeper than this, and one can get an appreciation of it only from a thorough examination of the various facts that make it up.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 122.
People were pretty well spellbound by what Bohr said… While I was very much impressed by [him], his arguments were mainly of a qualitative nature, and I was not able to really pinpoint the facts behind them. What I wanted was statements which could be expressed in terms of equations, and Bohr's work very seldom provided such statements. I am really not sure how much later my work was influenced by these lectures of Bohr's... He certainly did not have a direct influence because he did not stimulate one to think of new equations.
Recalling the occasion in May 1925 (a year before receiving his Ph.D.) when he met Niels Bohr who was in Cambridge to give a talk on the fundamental difficulties of the quantum theory.
Recalling the occasion in May 1925 (a year before receiving his Ph.D.) when he met Niels Bohr who was in Cambridge to give a talk on the fundamental difficulties of the quantum theory.
— Paul A. M. Dirac
In History of Twentieth Century Physics (1977), 109. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 94.
Pick a flower on Earth and you move the farthest star.
— Paul A. M. Dirac
As given, without citation, in Paul G. Hewitt, Conceptual Physics (4th ed., 1981), 51, footnote.
Pure mathematics and physics are becoming ever more closely connected, though their methods remain different. One may describe the situation by saying that the mathematician plays a game in which he himself invents the rules while the while the physicist plays a game in which the rules are provided by Nature, but as time goes on it becomes increasingly evident that the rules which the mathematician finds interesting are the same as those which Nature has chosen. … Possibly, the two subjects will ultimately unify, every branch of pure mathematics then having its physical application, its importance in physics being proportional to its interest in mathematics.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 124.
The fundamental laws necessary for the mathematical treatment of a large part of physics and the whole of chemistry are thus completely known, and the difficulty lies only in the fact that application of these laws leads to equations that are too complex to be solved.
— Paul A. M. Dirac
'Quantum Mechanics of Many-Electron Systems', Proceedings of the Royal Society (1929), A, 123, 714-733. Quoted in Steven M. Bachrach, Computational Organic Chemistry, Preface, xiii.
The mathematician plays a game in which he himself invents the rules while the physicist plays a game in which the rules are provided by nature, but as time goes on it becomes increasingly evident that the rules which the mathematician finds interesting are the same as those which nature has chosen.
— Paul A. M. Dirac
In Ian Stewart, Why Beauty is Truth (2007), 279.
The methods of theoretical physics should be applicable to all those branches of thought in which the essential features are expressible with numbers.
— Paul A. M. Dirac
Nobel Prize Banquet Speech (10 Dec1933). In Carl Gustaf Santesson (Ed.), Les Prix Nobel en 1933 (1935), 78
The only object of theoretical physics is to calculate results that can be compared with experiment... it is quite unnecessary that any satisfactory description of the whole course of the phenomena should be given.
— Paul A. M. Dirac
The Principles of Quantum Mechanics (1930), 7.
The physicist, in his study of natural phenomena, has two methods of making progress: (1) the method of experiment and observation, and (2) the method of mathematical reasoning. The former is just the collection of selected data; the latter enables one to infer results about experiments that have not been performed. There is no logical reason why the second method should be possible at all, but one has found in practice that it does work and meets with reasonable success.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 122.
The research worker, in his efforts to express the fundamental laws of Nature in mathematical form, should strive mainly for mathematical beauty. He should take simplicity into consideration in a subordinate way to beauty. It often happens that the requirements of simplicity and beauty are the same, but where they clash, the latter must take precedence.
— Paul A. M. Dirac
From Proceedings of the Royal Society of Edinburgh (1939), 59 122. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 110.
The steady progress of physics requires for its theoretical formulation a mathematics which get continually more advanced. ... it was expected that mathematics would get more and more complicated, but would rest on a permanent basis of axioms and definitions, while actually the modern physical developments have required a mathematics that continually shifts its foundation and gets more abstract. Non-euclidean geometry and noncommutative algebra, which were at one time were considered to be purely fictions of the mind and pastimes of logical thinkers, have now been found to be very necessary for the description of general facts of the physical world. It seems likely that this process of increasing abstraction will continue in the future and the advance in physics is to be associated with continual modification and generalisation of the axioms at the base of mathematics rather than with a logical development of any one mathematical scheme on a fixed foundation.
— Paul A. M. Dirac
Introduction to a paper on magnetic monopoles, 'Quantised singularities in the electromagnetic field', Proceedings of the Royal Society of Lonndon (1931), A, 133 60. In Helge Kragh, Dirac: a Scientific Biography (1990), 208.
The trend of mathematics and physics towards unification provides the physicist with a powerful new method of research into the foundations of his subject. … The method is to begin by choosing that branch of mathematics which one thinks will form the basis of the new theory. One should be influenced very much in this choice by considerations of mathematical beauty. It would probably be a good thing also to give a preference to those branches of mathematics that have an interesting group of transformations underlying them, since transformations play an important role in modern physical theory, both relativity and quantum theory seeming to show that transformations are of more fundamental importance than equations.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 122.
Theoretical physicists accept the need for mathematical beauty as an act of faith... For example, the main reason why the theory of relativity is so universally accepted is its mathematical beauty.
— Paul A. M. Dirac
'Methods in Theoretical Physics', From A Life of Physics: Evening Lectures at the International Centre for Theoretical Physics, Trieste, Italy. A Special Supplement of the IAEA Bulletin (1968), 22.
There are, at present, fundamental problems in theoretical physics … the solution of which … will presumably require a more drastic revision of our fundmental concepts than any that have gone before. Quite likely, these changes will be so great that it will be beyond the power of human intelligence to get the necessary new ideas by direct attempts to formulate the experimental data in mathematical terms. The theoretical worker in the future will, therefore, have to proceed in a more direct way. The most powerful method of advance that can be suggested at present is to employ all the resources of pure mathematics in attempts to perfect and generalize the mathematical formalism that forms the existing basis of theoretical physics, and after each success in this direction, to try to interpret the new mathematical features in terms of physical entities.
At age 28.
At age 28.
— Paul A. M. Dirac
Proceedings of the Royal Society (1931), A133, 60. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 109.
There is thus a possibility that the ancient dream of philosophers to connect all Nature with the properties of whole numbers will some day be realized. To do so physics will have to develop a long way to establish the details of how the correspondence is to be made. One hint for this development seems pretty obvious, namely, the study of whole numbers in modern mathematics is inextricably bound up with the theory of functions of a complex variable, which theory we have already seen has a good chance of forming the basis of the physics of the future. The working out of this idea would lead to a connection between atomic theory and cosmology.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 129.
We must regard it rather as an accident that the Earth (and presumably the whole solar system) contains a preponderance of negative electrons and positive protons. It is quite possible that for some of the stars it is the other way about.
— Paul A. M. Dirac
(1902)
Well, in the first place, it leads to great anxiety as to whether it’s going to be correct or not … I expect that’s the dominating feeling. It gets to be rather a fever…
At age 60, when asked about his feelings on discovering the Dirac equation.
At age 60, when asked about his feelings on discovering the Dirac equation.
— Paul A. M. Dirac
"Interview with T. Kuhn (7 May 1963), Niels Bohr Library, American Intitute of Physics, New York. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 110.
What makes the theory of relativity so acceptable to physicists in spite of its going against the principle of simplicity is its great mathematical beauty. This is a quality which cannot be defined, any more than beauty in art can be defined, but which people who study mathematics usually have no difficulty in appreciating. … The restricted theory changed our ideas of space and time in a way that may be summarised by stating that the group of transformations to which the space-time continuum is subject must be changed from the Galilean group to the Lorentz group.
— Paul A. M. Dirac
From Lecture delivered on presentation of the James Scott prize, (6 Feb 1939), 'The Relation Between Mathematics And Physics', printed in Proceedings of the Royal Society of Edinburgh (1938-1939), 59, Part 2, 123.
When [Erwin Schrödinger] went to the Solvay conferences in Brussels, he would walk from the station to the hotel where the delegates stayed, carrying all his luggage in a rucksack and looking so like a tramp that it needed a great deal of argument at the reception desk before he could claim a room.
— Paul A. M. Dirac
Quoted in Robert L. Weber, Pioneers of Science: Nobel Prize Winners in Physics (1980), 100.
When an observation is made on any atomic system that has been prepared in a given way and is thus in a given state, the result will not in general be determinate, i.e. if the experiment is repeated several times under identical conditions several different results may be obtained. If the experiment is repeated a large number of times it will be found that each particular result will be obtained a definite fraction of the total number of times, so that one can say there is a definite probability of its being obtained any time that the experiment is performed. This probability the theory enables one to calculate. (1930)
— Paul A. M. Dirac
The Principles of Quantum Mechanics 4th ed. (1981), 13-14
When we make the photon meet a tourmaline crystal, we are subjecting it to an observation. We are observing whether it is polarised parallel or perpendicular to the optic axis. The effect of making the observation is to force the photon entirely into the state of perpendicular polarisation. It has to make a sudden jump from being partly in each of these two states to being entirely in one or other of them. Which of the two states it will jump into cannot be predicted, but is governed only by probability laws. If it jumps into the perpendicular state it passes through the crystal and appears on the other side preserving this state of polarisation.
— Paul A. M. Dirac
The Principles of Quantum Mechanics (1930).
Quotes by others about Paul A. M. Dirac (5)
Dirac politely refused Robert’s [Robert Oppenheimer] two proffered books: reading books, the Cambridge theoretician announced gravely, “interfered with thought.”
Alvarez: Adventures of a Physicist (1987), 87.
If this is what the McCarran Act means in practice, it seems to us a form of organized cultural suicide.
In a letter co-signed with his Princeton University physics professor colleagues, Walker Bleakney and Milton G. White, protesting that Nobel Prize-winning, Cambridge professor, Dirac having been invited for a year's visit to Princeton, had been denied a visa by the U.S. State Department under section 212A of the Immigration and Naturalization Act (McCarran Act). Quoting a report in Physics Today, this regulation includes 'categories of undesireables ranging from vagrants to stowaways.' The real reason remains unclear, but was perhaps related to Dirac's prior science-related visits to Russia. Robert Oppenheimer's security clearance had recently been revoked, and this was the era of McCarthy's rabid anti-Communism hearings.
In a letter co-signed with his Princeton University physics professor colleagues, Walker Bleakney and Milton G. White, protesting that Nobel Prize-winning, Cambridge professor, Dirac having been invited for a year's visit to Princeton, had been denied a visa by the U.S. State Department under section 212A of the Immigration and Naturalization Act (McCarran Act). Quoting a report in Physics Today, this regulation includes 'categories of undesireables ranging from vagrants to stowaways.' The real reason remains unclear, but was perhaps related to Dirac's prior science-related visits to Russia. Robert Oppenheimer's security clearance had recently been revoked, and this was the era of McCarthy's rabid anti-Communism hearings.
'Letters to the Times: Denial of Visa to Physicist Seen as Loss to American Science'. New York Times (3 Jun 1954), 26. In A. Pais, 'Playing With Equations, the Dirac Way'. Behram N. Kursunoglu (Ed.) and Eugene Paul Wigner (Ed.), Paul Adrien Maurice Dirac: Reminiscences about a Great Physicist (1990), 108.
But, contrary to the lady’s prejudices about the engineering profession, the fact is that quite some time ago the tables were turned between theory and applications in the physical sciences. Since World War II the discoveries that have changed the world are not made so much in lofty halls of theoretical physics as in the less-noticed labs of engineering and experimental physics. The roles of pure and applied science have been reversed; they are no longer what they were in the golden age of physics, in the age of Einstein, Schrödinger, Fermi and Dirac.
'The Age of Computing: a Personal Memoir', Daedalus (1992), 121, 120.
I count Maxwell and Einstein, Eddington and Dirac, among “real” mathematicians. The great modern achievements of applied mathematics have been in relativity and quantum mechanics, and these subjects are at present at any rate, almost as “useless” as the theory of numbers.
In A Mathematician's Apology (1940, 2012), 131.
Mathematical theories have sometimes been used to predict phenomena that were not confirmed until years later. For example, Maxwell’s equations, named after physicist James Clerk Maxwell, predicted radio waves. Einstein’s field equations suggested that gravity would bend light and that the universe is expanding. Physicist Paul Dirac once noted that the abstract mathematics we study now gives us a glimpse of physics in the future. In fact, his equations predicted the existence of antimatter, which was subsequently discovered. Similarly, mathematician Nikolai Lobachevsky said that “there is no branch of mathematics, however abstract, which may not someday be applied to the phenomena of the real world.”
In 'Introduction', The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (2009), 12.
See also:
- 8 Aug - short biography, births, deaths and events on date of Dirac's birth.
- The Strangest Man: The Hidden Life of Paul Dirac, Mystic of the Atom, by Graham Farmelo. - book suggestion.
- Booklist for Paul Dirac.
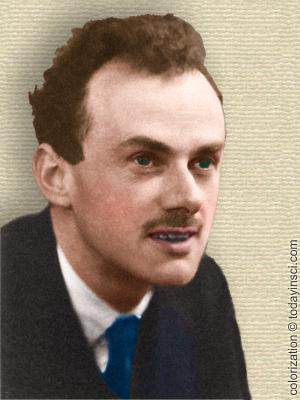










 In science it often happens that scientists say, 'You know that's a really good argument; my position is mistaken,' and then they would actually change their minds and you never hear that old view from them again. They really do it. It doesn't happen as often as it should, because scientists are human and change is sometimes painful. But it happens every day. I cannot recall the last time something like that happened in politics or religion.
(1987) --
In science it often happens that scientists say, 'You know that's a really good argument; my position is mistaken,' and then they would actually change their minds and you never hear that old view from them again. They really do it. It doesn't happen as often as it should, because scientists are human and change is sometimes painful. But it happens every day. I cannot recall the last time something like that happened in politics or religion.
(1987) -- 


