|
Ptolemy
(c. 100 - c. 170)
Greek astronomer who wrote the famous book of mathematical astronomy, known as the Almagest, which described the Ptolemaic (geocentric) universe.
|
PTOLEMY.
from Great Astronomers (1901)
The career of the famous man whose name stands at the head of this chapter is one of the most remarkable in the history of human learning. There may have been other discoverers who have done more for science than ever Ptolemy accomplished, but there never has been any other discoverer whose authority on the subject of the movements of the heavenly bodies has held sway over the minds of men for so long a period as the fourteen centuries during which his opinions reigned supreme. The doctrines he laid down in his famous book, “The Almagest,” prevailed throughout those ages. No substantial addition was made in all that time to the undoubted truths which this work contained. No important correction was made of the serious errors with which Ptolemy’s theories were contaminated. The authority of Ptolemy as to all things in the heavens, and as to a good many things on the earth (for the same illustrious man was also a diligent geographer), was invariably final.
Though every child may now know more of the actual truths of the celestial motions than ever Ptolemy knew, yet the fact that his work exercised such an astonishing effect on the human intellect for some sixty generations, shows that it must have been an extraordinary production. We must look into the career of this wonderful man to discover wherein lay the secret of that marvellous success which made him the unchallenged instructor of the human race for such a protracted period.
Unfortunately, we know very little as to the personal history of Ptolemy. He was a native of Egypt, and though it has been sometimes conjectured that he belonged to the royal families of the same name, yet there is nothing to support such a belief. The name, Ptolemy, appears to have been a common one in Egypt in those days. The time at which he lived is fixed by the fact that his first recorded observation was made in 127 AD, and his last in 151 AD. When we add that he seems to have lived in or near Alexandria, or to use his own words, “on the parallel of Alexandria,” we have said everything that can be said so far as his individuality is concerned.
Ptolemy is, without doubt, the greatest figure in ancient astronomy. He gathered up the wisdom of the philosophers who had preceded him. He incorporated this with the results of his own observations, and illumined it with his theories. His speculations, even when they were, as we now know, quite erroneous, had such an astonishing verisimilitude to the actual facts of nature that they commanded universal assent. Even in these modern days we not unfrequently find lovers of paradox who maintain that Ptolemy’s doctrines not only seem true, but actually are true.
In the absence of any accurate knowledge of the science of mechanics, philosophers in early times were forced to fall back on certain principles of more or less validity, which they derived from their imagination as to what the natural fitness of things ought to be. There was no geometrical figure so simple and so symmetrical as a circle, and as it was apparent that the heavenly bodies pursued tracks which were not straight lines, the conclusion obviously followed that their movements ought to be circular. There was no argument in favour of this notion, other than the merely imaginary reflection that circular movement, and circular movement alone, was “perfect,” whatever “perfect” may have meant. It was further believed to be impossible that the heavenly bodies could have any other movements save those which were perfect. Assuming this, it followed, in Ptolemy’s opinion, and in that of those who came after him for fourteen centuries, that all the tracks of the heavenly bodies were in some way or other to be reduced to circles.
Ptolemy succeeded in devising a scheme by which the apparent changes that take place in the heavens could, so far as he knew them, be explained by certain combinations of circular movement. This seemed to reconcile so completely the scheme of things celestial with the geometrical instincts which pointed to the circle as the type of perfect movement, that we can hardly wonder Ptolemy’s theory met with the astonishing success that attended it. We shall, therefore, set forth with sufficient detail the various steps of this famous doctrine.
Ptolemy commences with laying down the undoubted truth that the shape of the earth is globular. The proofs which he gives of this fundamental fact are quite satisfactory; they are indeed the same proofs as we give today. There is, first of all, the well-known circumstance of which our books on geography remind us, that when an object is viewed at a distance across the sea, the lower part of the object appears cut off by the interposing curved mass of water.
The sagacity of Ptolemy enabled him to adduce another argument, which, though not quite so obvious as that just mentioned, demonstrates the curvature of the earth in a very impressive manner to anyone who will take the trouble to understand it. Ptolemy mentions that travellers who went to the south reported, that, as they did so, the appearance of the heavens at night underwent a gradual change. Stars that they were familiar with in the northern skies gradually sank lower in the heavens. The constellation of the Great Bear, which in our skies never sets during its revolution round the pole, did set and rise when a sufficient southern latitude had been attained. On the other hand, constellations new to the inhabitants of northern climes were seen to rise above the southern horizon. These circumstances would be quite incompatible with the supposition that the earth was a flat surface. Had this been so, a little reflection will show that no such changes in the apparent movements of the stars would be the consequence of a voyage to the south. Ptolemy set forth with much insight the significance of this reasoning, and even now, with the resources of modern discoveries to help us, we can hardly improve upon his arguments.
Ptolemy, like a true philosopher disclosing a new truth to the world, illustrated and enforced his subject by a variety of happy demonstrations. I must add one of them, not only on account of its striking nature, but also because it exemplifies Ptolemy’s acuteness. If the earth were flat, said this ingenious reasoner, sunset must necessarily take place at the same instant, no matter in what country the observer may happen to be placed. Ptolemy, however, proved that the time of sunset did vary greatly as the observer’s longitude was altered. To us, of course, this is quite obvious; everybody knows that the hour of sunset may have been reached in Great Britain while it is still noon on the western coast of America. Ptolemy had, however, few of those sources of knowledge which are now accessible. How was he to show that the sun actually did set earlier at Alexandria than it would in a city which lay a hundred miles to the west? There was no telegraph wire by which astronomers at the two Places could communicate. There was no chronometer or watch which could be transported from place to place; there was not any other reliable contrivance for the keeping of time. Ptolemy’s ingenuity, however, pointed out a thoroughly satisfactory method by which the times of sunset at two places could be compared. He was acquainted with the fact, which must indeed have been known from the very earliest times, that the illumination of the moon is derived entirely from the sun. He knew that an eclipse of the moon was due to the interposition of the earth which cuts off the light of the sun. It was, therefore, plain that an eclipse of the moon must be a phenomenon which would begin at the same instant from whatever part of the earth the moon could be seen at the time. Ptolemy, therefore, brought together from various quarters the local times at which different observers had recorded the beginning of a lunar eclipse. He found that the observers to the west made the time earlier and earlier the further away their stations were from Alexandria. On the other hand, the eastern observers set down the hour as later than that at which the phenomenon appeared at Alexandria. As these observers all recorded something which indeed appeared to them simultaneously, the only interpretation was, that the more easterly a place the later its time. Suppose there were a number of observers along a parallel of latitude, and each noted the hour of sunset to be six o’clock, then, since the eastern times are earlier than western times, 6 p.m. at one station A will correspond to 5 p.m. at a station B sufficiently to the west. If, therefore, it is sunset to the observer at A, the hour of sunset will not yet be reached for the observer at B. This proves conclusively that the time of sunset is not the same all over the earth. We have, however, already seen that the apparent time of sunset would be the same from all stations if the earth were flat. When Ptolemy, therefore, demonstrated that the time of sunset was not the same at various places, he showed conclusively that the earth was not flat.
As the same arguments applied to all parts of the earth where Ptolemy had either been himself, or from which he could gain the necessary information, it followed that the earth, instead of being the flat plain, girdled with an illimitable ocean, as was generally supposed, must be in reality globular. This led at once to a startling consequence. It was obvious that there could be no supports of any kind by which this globe was sustained; it therefore followed that the mighty object must be simply poised in space. This is indeed an astonishing doctrine to anyone who relies on what merely seems the evidence of the senses, without giving to that evidence its due intellectual interpretation. According to our ordinary experience, the very idea of an object poised without support in space, appears preposterous. Would it not fall? we are immediately asked. Yes, doubtless it could not remain poised in any way in which we try the experiment. We must, however, observe that there are no such ideas as upwards or downwards in relation to open space. To say that a body falls downwards, merely means that it tries to fall as nearly as possible towards the centre of the earth. There is no one direction along which a body will tend to move in space, in preference to any other. This may be illustrated by the fact that a stone let fall at New Zealand will, in its approach towards the earth’s centre, be actually moving upwards as far as any locality in our hemisphere is concerned. Why, then, argued Ptolemy, may not the earth remain poised in space, for as all directions are equally upward or equally downward, there seems no reason why the earth should require any support? By this reasoning he arrives at the fundamental conclusion that the earth is a globular body freely lying in space, and surrounded above, below, and on all sides by the glittering stars of heaven.
The perception of this sublime truth marks a notable epoch in the history of the gradual development of the human intellect. No doubt, other philosophers, in groping after knowledge, may have set forth certain assertions that are more or less equivalent to this fundamental truth. It is to Ptolemy we must give credit, however, not only for announcing this doctrine, but for demonstrating it by clear and logical argument. We cannot easily project our minds back to the conception of an intellectual state in which this truth was unfamiliar. It may, however, be well imagined that, to one who thought the earth was a flat plain of indefinite extent, it would be nothing less than an intellectual convulsion for him to be forced to believe that he stood upon a spherical earth, forming merely a particle relatively to the immense sphere of the heavens.
What Ptolemy saw in the movements of the stars led him to the conclusion that they were bright points attached to the inside of a tremendous globe. The movements of this globe which carried the stars were only compatible with the supposition that the earth occupied its centre. The imperceptible effect produced by a change in the locality of the observer on the apparent brightness of the stars made it plain that the dimensions of the terrestrial globe must be quite insignificant in comparison with those of the celestial sphere. The earth might, in fact, be regarded as a grain of sand while the stars lay upon a globe many yards in diameter.
So tremendous was the revolution in human knowledge implied by this discovery, that we can well imagine how Ptolemy, dazzled as it were by the fame which had so justly accrued to him, failed to make one further step. Had he made that step, it would have emancipated the human intellect from the bondage of fourteen centuries of servitude to a wholly monstrous notion of this earth’s importance in the scheme of the heavens. The obvious fact that the sun, the moon, and the stars rose day by day, moved across the sky in a glorious never-ending procession, and duly set when their appointed courses had been run, demanded some explanation. The circumstance that the fixed stars preserved their mutual distances from year to year, and from age to age, appeared to Ptolemy to prove that the sphere which contained those stars, and on whose surface they were believed by him to be fixed, revolved completely around the earth once every day. He would thus account for all the phenomena of rising and setting consistently with the supposition that our globe was stationary. Probably this supposition must have appeared monstrous, even to Ptolemy. He knew that the earth was a gigantic object, but, large as it may have been, he knew that it was only a particle in comparison with the celestial sphere, yet he apparently believed, and certainly succeeded in persuading other men to believe, that the celestial sphere did actually perform these movements.
Ptolemy was an excellent geometer. He knew that the rising and the setting of the sun, the moon, and the myriad stars, could have been accounted for in a different way. If the earth turned round uniformly once a day while poised at the centre of the sphere of the heavens, all the phenomena of rising and setting could be completely explained. This is, indeed, obvious after a moment’s reflection. Consider yourself to be standing on the earth at the centre of the heavens. There are stars over your head, and half the contents of the heavens are visible, while the other half are below your horizon. As the earth turns round, the stars over your head will change, and unless it should happen that you have taken up your position at either of the poles, new stars will pass into your view, and others will disappear, for at no time can you have more than half of the whole sphere visible. The observer on the earth would, therefore, say that some stars were rising, and that some stars were setting. We have, therefore, two totally distinct methods, each of which would completely explain all the observed facts of the diurnal movement. One of these suppositions requires that the celestial sphere, bearing with it the stars and other celestial bodies, turns uniformly around an invisible axis, while the earth remains stationary at the centre. The other supposition would be, that it is the stupendous celestial sphere which remains stationary, while the earth at the centre rotates about the same axis as the celestial sphere did before, but in an opposite direction, and with a uniform velocity which would enable it to complete one turn in twenty-four hours. Ptolemy was mathematician enough to know that either of these suppositions would suffice for the explanation of the observed facts. Indeed, the phenomena of the movements of the stars, so far as he could observe them, could not be called upon to pronounce which of these views was true, and which was false.
Ptolemy had, therefore, to resort for guidance to indirect lines of reasoning. One of these suppositions must be true, and yet it appeared that the adoption of either was accompanied by a great difficulty. It is one of his chief merits to have demonstrated that the celestial sphere was so stupendous that the earth itself was absolutely insignificant in comparison therewith. If, then, this stupendous sphere rotated once in twenty-four hours, the speed with which the movement of some of the stars must be executed would be so portentous as to seem well-nigh impossible. It would, therefore, seem much simpler on this ground to adopt the other alternative, and to suppose the diurnal movements were due to the rotation of the earth. Here Ptolemy saw, or at all events fancied he saw, objections of the weightiest description. The evidence of the senses appeared directly to controvert the supposition that this earth is anything but stationary. Ptolemy might, perhaps, have dismissed this objection on the ground that the testimony of the senses on such a matter should be entirely subordinated to the interpretation which our intelligence would place upon the facts to which the senses deposed. Another objection, however, appeared to him to possess the gravest moment. It was argued that if the earth were rotating, there is nothing to make the air participate in this motion, mankind would therefore be swept from the earth by the furious blasts which would arise from the movement of the earth through an atmosphere at rest. Even if we could imagine that the air were carried round with the earth, the same would not apply, so thought Ptolemy, to any object suspended in the air. So long as a bird was perched on a tree, he might very well be carried onward by the moving earth, but the moment he took wing, the ground would slip from under him at a frightful pace, so that when he dropped down again he would find himself at a distance perhaps ten times as great as that which a carrier-pigeon or a swallow could have traversed in the same time. Some vague delusion of this description seems even still to crop up occasionally. I remember hearing of a proposition for balloon travelling of a very remarkable kind. The voyager who wanted to reach any other place in the same latitude was simply to ascend in a balloon, and wait there till the rotation of the earth conveyed the locality which happened to be his destination directly beneath him, whereupon he was to let out the gas and drop down! Ptolemy knew quite enough natural philosophy to be aware that such a proposal for locomotion would be an utter absurdity; he knew that there was no such relative shift between the air and the earth as this motion would imply. It appeared to him to be necessary that the air should lag behind, if the earth had been animated by a movement of rotation. In this he was, as we know, entirely wrong. There were, however, in his days no accurate notions on the subject of the laws of motion.
Assiduous as Ptolemy may have been in the study of the heavenly bodies, it seems evident that he cannot have devoted much thought to the phenomena of motion of terrestrial objects. Simple, indeed, are the experiments which might have convinced a philosopher much less acute than Ptolemy, that, if the earth did revolve, the air must necessarily accompany it. If a rider galloping on horseback tosses a ball into the air, it drops again into his hand, just as it would have done had he been remaining at rest during the ball’s flight; the ball in fact participates in the horizontal motion, so that though it really describes a curve as any passer-by would observe, yet it appears to the rider himself merely to move up and down in a straight line. This fact, and many others similar to it, demonstrate clearly that if the earth were endowed with a movement of rotation, the atmosphere surrounding it must participate in that movement. Ptolemy did not know this, and consequently he came to the conclusion that the earth did not rotate, and that, therefore, notwithstanding the tremendous improbability of so mighty an object as the celestial sphere spinning round once in every twenty-four hours, there was no course open except to believe that this very improbable thing did really happen. Thus it came to pass that Ptolemy adopted as the cardinal doctrine of his system a stationary earth poised at the centre of the celestial sphere, which stretched around on all sides at a distance so vast that the diameter of the earth was an inappreciable point in comparison therewith.
Ptolemy having thus deliberately rejected the doctrine of the earth’s rotation, had to make certain other entirely erroneous suppositions. It was easily seen that each star required exactly the same period for the performance of a complete revolution of the heavens. Ptolemy knew that the stars were at enormous distances from the earth, though no doubt his notions on this point came very far short of what we know to be the reality. If the stars had been at very varied distances, then it would be so wildly improbable that they should all accomplish their revolutions in the same time, that Ptolemy came to the conclusion that they must be all at the same distance, that is, that they must be all on the surface of a sphere. This view, however erroneous, was corroborated by the obvious fact that the stars in the constellations preserved their relative places unaltered for centuries. Thus it was that Ptolemy came to the conclusion that they were all fixed on one spherical surface, though we are not informed as to the material of this marvellous setting which sustained the stars like jewels.
Nor should we hastily pronounce this doctrine to be absurd. The stars do appear to lie on the surface of a sphere, of which the observer is at the centre; not only is this the aspect which the skies present to the untechnical observer, but it is the aspect in which the skies are presented to the most experienced astronomer of modern days. No doubt he knows well that the stars are at the most varied distances from him; he knows that certain stars are ten times, or a hundred times, or a thousand times, as far as other stars. Nevertheless, to his eye the stars appear on the surface of the sphere, it is on that surface that his measurements of the relative places of the stars are made; indeed, it may be said that almost all the accurate observations in the observatory relate to the places of the stars, not as they really are, but as they appear to be projected on that celestial sphere whose conception we owe to the genius of Ptolemy.
This great philosopher shows very ingeniously that the earth must be at the centre of the sphere. He proves that, unless this were the case, each star would not appear to move with the absolute uniformity which does, as a matter of fact, characterise it. In all these reasonings we cannot but have the most profound admiration for the genius of Ptolemy, even though he had made an error so enormous in the fundamental point of the stability of the earth. Another error of a somewhat similar kind seemed to Ptolemy to be demonstrated. He had shown that the earth was an isolated object in space, and being such was, of course, capable of movement. It could either be turned round, or it could be moved from one place to another. We know that Ptolemy deliberately adopted the view that the earth did not turn round; he had then to investigate the other question, as to whether the earth was animated by any movement of translation. He came to the conclusion that to attribute any motion to the earth would be incompatible with the truths at which he had already arrived. The earth, argued Ptolemy, lies at the centre of the celestial sphere. If the earth were to be endowed with movement, it would not lie always at this point, it must, therefore, shift to some other part of the sphere. The movements of the stars, however, preclude the possibility of this; and, therefore, the earth must be as devoid of any movement of translation as it is devoid of rotation. Thus it was that Ptolemy convinced himself that the stability of the earth, as it appeared to the ordinary senses, had a rational philosophical foundation.
Not unfrequently it is the lot of the philosophers to contend against the doctrines of the vulgar, but when it happens, as in the case of Ptolemy’s researches, that the doctrines of the vulgar are corroborated by philosophical investigation which bear the stamp of the highest authority, it is not to be wondered at that such doctrines should be deemed well-nigh impregnable. In this way we may, perhaps, account for the remarkable fact that the theories of Ptolemy held unchallenged sway over the human intellect for the vast period already mentioned.
Up to the present we have been speaking only of those primary motions of the heavens, by which the whole sphere appeared to revolve once every twenty-four hours. We have now to discuss the remarkable theories by which Ptolemy endeavoured to account for the monthly movement of the moon, for the annual movement of the sun, and for the periodic movements of the planets which had gained for them the titles of the wandering stars.
Possessed with the idea that these movements must be circular, or must be capable, directly or indirectly, of being explained by circular movements, it seemed obvious to Ptolemy, as indeed it had done to previous astronomers, that the track of the moon through the stars was a circle of which the earth is the centre. A similar movement with a yearly period must also be attributed to the sun, for the changes in the positions of the constellations in accordance with the progress of the seasons, placed it beyond doubt that the sun made a circuit of the celestial sphere, even though the bright light of the sun prevented the stars in its vicinity, from being seen in daylight. Thus the movements both of the sun and the moon, as well as the diurnal rotation of the celestial sphere, seemed to justify the notion that all celestial movements must be “perfect,” that is to say, described uniformly in those circles which were the only perfect curves.
The simplest observations, however, show that the movements of the planets cannot be explained in this simple fashion. Here the geometrical genius of Ptolemy shone forth, and he devised a scheme by which the apparent wanderings of the planets could be accounted for without the introduction of aught save “perfect” movements.
To understand his reasoning, let us first set forth clearly those facts of observation which require to be explained. I shall take, in particular, two planets, Venus and Mars, as these illustrate, in the most striking manner, the peculiarities of the inner and the outer planets respectively. The simplest observations would show that Venus did not move round the heavens in the same fashion as the sun or the moon. Look at the evening star when brightest, as it appears in the west after sunset. Instead of moving towards the east among the stars, like the sun or the moon, we find, week after week, that Venus is drawing in towards the sun, until it is lost in the sunbeams. Then the planet emerges on the other side, not to be seen as an evening star, but as a morning star. In fact, it was plain that in some ways Venus accompanied the sun in its annual movement. Now it is found advancing in front of the sun to a certain limited distance, and now it is lagging to an equal extent behind the sun.
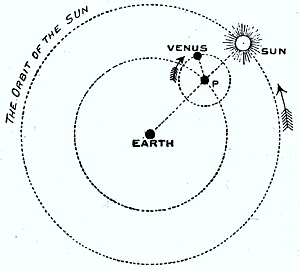
These movements were wholly incompatible with the supposition that the journeys of Venus were described by a single motion of the kind regarded as perfect. It was obvious that the movement was connected in some strange manner with the revolution of the sun, and here was the ingenious method by which Ptolemy sought to render account of it. Imagine a fixed arm to extend from the earth to the sun, as shown in the accompanying figure (Fig. 1), then this arm will move round uniformly, in consequence of the sun’s movement. At a point P on this arm let a small circle be described. Venus is supposed to revolve uniformly in this small circle, while the circle itself is carried round continuously by the movement of the sun. In this way it was possible to account for the chief peculiarities in the movement of Venus. It will be seen that, in consequence of the revolution around P, the spectator on the earth will sometimes see Venus on one side of the sun, and sometimes on the other side, so that the planet always remains in the sun’s vicinity. By properly proportioning the movements, this little contrivance simulated the transitions from the morning star to the evening star. Thus the changes of Venus could be accounted for by a Combination of the “perfect” movement of P in the circle which it described uniformly round the earth, combined with the “perfect” motion of Venus in the circle which it described uniformly around the moving centre.
In a precisely similar manner Ptolemy rendered an explanation of the fitful apparitions of Mercury. Now just on one side of the sun, and now just on the other, this rarely-seen planet moved like Venus on a circle whereof the centre was also carried by the line joining the sun and the earth. The circle, however, in which Mercury actually revolved had to be smaller than that of Venus, in order to account for the fact that Mercury lies always much closer to the sun than the better-known planet.
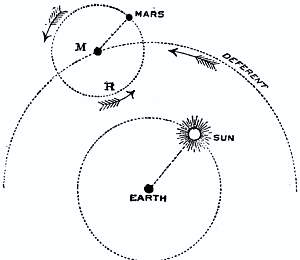
The explanation of the movement of an outer planet like Mars could also be deduced from the joint effect of two perfect motions. The changes through which Mars goes are, however, so different from the movements of Venus that quite a different disposition of the circles is necessary. For consider the facts which characterise the movements of an outer planet such as Mars. In the first place, Mars accomplishes an entire circuit of the heaven. In this respect, no doubt, it may be said to resemble the sun or the moon. A little attention will, however, show that there are extraordinary irregularities in the movement of the planet. Generally speaking, it speeds its way from west to east among the stars, but sometimes the attentive observer will note that the speed with which the planet advances is slackening, and then it will seem to become stationary. Some days later the direction of the planet’s movement will be reversed, and it will be found moving from the east towards the west. At first it proceeds slowly and then quickens its pace, until a certain speed is attained, which afterwards declines until a second stationary position is reached. After a due pause the original motion from west to east is resumed, and is continued until a similar cycle of changes again commences. Such movements as these were obviously quite at variance with any perfect movement in a single circle round the earth. Here, again, the geometrical sagacity of Ptolemy provided him with the means of representing the apparent movements of Mars, and, at the same time, restricting the explanation to those perfect movements which he deemed so essential. In Fig. 2 we exhibit Ptolemy’s theory as to the movement of Mars. We have, as before, the earth at the centre, and the sun describing its circular orbit around that centre. The path of Mars is to be taken as exterior to that of the sun. We are to suppose that at a point marked M there is a fictitious planet, which revolves around the earth uniformly, in a circle called the DEFERENT. This point M, which is thus animated by a perfect movement, is the centre of a circle which is carried onwards with M, and around the circumference of which Mars revolves uniformly. It is easy to show that the combined effect of these two perfect movements is to produce exactly that displacement of Mars in the heavens which observation discloses. In the position represented in the figure, Mars is obviously pursuing a course which will appear to the observer as a movement from west to east. When, however, the planet gets round to such a position as R, it is then moving from east to west in consequence of its revolution in the moving circle, as indicated by the arrow-head. On the other hand, the whole circle is carried forward in the opposite direction. If the latter movement be less rapid than the former, then we shall have the backward movement of Mars on the heavens which it was desired to explain. By a proper adjustment of the relative lengths of these arms the movements of the planet as actually observed could be completely accounted for.
The other outer planets with which Ptolemy was acquainted, namely, Jupiter and Saturn, had movements of the same general character as those of Mars. Ptolemy was equally successful in explaining the movements they performed by the supposition that each planet had perfect rotation in a circle of its own, which circle itself had perfect movement around the earth in the centre.
It is somewhat strange that Ptolemy did not advance one step further, as by so doing he would have given great simplicity to his system. He might, for instance, have represented the movements of Venus equally well by putting the centre of the moving circle at the sun itself, and correspondingly enlarging the circle in which Venus revolved. He might, too, have arranged that the several circles which the outer planets traversed should also have had their centres at the sun. The planetary system would then have consisted of an earth fixed at the centre, of a sun revolving uniformly around it, and of a system of planets each describing its own circle around a moving centre placed in the sun. Perhaps Ptolemy had not thought of this, or perhaps he may have seen arguments against it. This important step was, however, taken by Tycho. He considered that all the planets revolved around the sun in circles, and that the sun itself, bearing all these orbits, described a mighty circle around the earth. This point having been reached, only one more step would have been necessary to reach the glorious truths that revealed the structure of the solar system. That last step was taken by Copernicus.
- Science Quotes by Ptolemy.
- Ptolemy - context of quote “When I trace at my pleasure the windings” - Medium image (500 x 250 px)
- Ptolemy - context of quote “When I trace at my pleasure the windings” - Large image (800 x 400 px)
- Ptolemy’s Almagest, by Ptolemy translated by G.J. Toomer. - book suggestion.
- Booklist for Ptolemy.