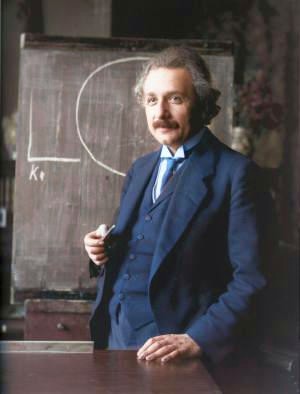(source)

Albert Einstein (14 Mar 1879 - 18 Apr 1955) German-American physicist who developed the special and general theories of relativity. He was awarded the 1921 Nobel Prize for Physics for his explanation of the photoelectric effect. Short biography of Albert Einstein >>

My Theory

by Albert Einstein

From The Times (28 Nov 1919)

Albert Einstein, Lecturing in Vienna, 1921. (source)

[p.41] After the lamentable breach in the former international relations existing among men of science, it is with joy and gratefulness that I accept this opportunity of communication with English astronomers and physicists. It was in accordance with the high and proud tradition of English science that English scientific men should have given their time and labor, and that English institutions should have provided the material means, to test a theory that had been completed and published in the country of their enemies in the midst of war. Although investigation of the influence of the solar gravitational field on rays of light is a purely objective matter, I am none the less very glad to express my personal thanks to my English colleagues in this branch of science; for without their aid I should not have obtained proof of the most vital deduction from my theory.

There are several kinds of theory in physics. Most of them are constructive. These attempt to build a picture of complex phenomena out of some relatively simple proposition. The kinetic theory of gases, for instance, attempts to refer to molecular movement the mechanical, thermal, and diffusional properties of gases. When we say that we understand a group of natural phenomena, we mean that we have found a constructive theory which embraces them.

But in addition to this most weighty group of theories, there is another group consisting of what I call theories of principle. These employ the analytic, not the synthetic method. Their starting point and foundation are not hypothetical constituents, but empirically observed general properties of phenomena, principles from which mathematical formula are deduced of such a kind that they apply to every case which presents itself. Thermodynamics, for instance, starting from the fact that perpetual motion never occurs in ordinary experience, attempts to deduce from this, by analytic processes, a theory which will apply in every case. The merit of constructive theories is their comprehensiveness, adaptability, and clarity; that of the theories of principle, their logical perfection, and the security of their foundation. The theory of relativity is a theory of principle. To understand it, the principles on which it rests must be grasped. But before stating these it is necessary to point out that the theory of relativity is like a house with two separate stories, the special relativity theory and the general theory of relativity.

Since the time of the ancient Greeks it has been well known that in describing the motion of a body we must refer to another body. The motion of a railway train is described with reference to the ground, of a planet with reference to the total assemblage of visible fixed stars. In physics the bodies to which motions are spatially referred are termed systems of coördinates. The laws of mechanics of Galileo and Newton can be formulated only by using a system of coördinates.

The state of motion of a system of [p.42] coördinates cannot be chosen arbitrarily if the laws of mechanics are to hold good (it must be free from twisting and from acceleration). The system of coördinates employed in mechanics is called an inertia system. The state of motion of an inertia system, so far as mechanics are concerned, is not restricted by nature to one condition. The condition in the following proposition suffices: a system of coördinates moving in the same direction and at the same rate as a system of inertia is itself a system of inertia. The special relativity theory is, therefore, the application of the following proposition to any natural process: ‘Every law of nature which holds good with respect to a coordinate system K must also hold good for any other system K', provided that K and K' are in uniform movement of translation.

The second principle on which the special relativity theory rests is that of the constancy of the velocity of light in a vacuum. Light in a vacuum has a definite and constant velocity, independent of the velocity of its source. Physicists owe their confidence in this proposition to the Maxwell-Lorentz theory of electro-dynamics.

The two principles which I have mentioned have received strong experimental confirmation but do not seem to be logically compatible. The special relativity theory achieved their logical reconciliation by making a change in kinematics, that is to say, in the doctrine of the physical laws of space and time. It became evident that a statement of the coincidence of two events could have a meaning only in connection with a system of coördinates; that the mass of bodies and the rate of movement of clocks must depend on their state of motion with regard to the coördinates.

But the older physics, including the laws of motion of Galileo and Newton, clashed with the relativistic kinematics that I have indicated. The latter gave origin to certain generalized mathematical conditions with which the laws of nature would have to conform if the two fundamental principles were compatible. Physics had to be modified. The most notable change was a new law of motion for (very rapidly) moving mass-points, and this soon came to be verified in the case of electrically-laden particles. The most important result of the special relativity system concerned the inert mass of a material system. It became evident that the inertia of such a system must depend on its energy content, so that we were driven to the conception that inert mass was nothing else than latent energy. The doctrine of the conservation of mass lost its independence and became merged in the doctrine of conservation of energy.

The special relativity theory, which was simply a systematic extension of the electro-dynamics of Maxwell and Lorentz, had consequences which reached beyond itself. Must the independence of physical laws with regard to a system of coördinates be limited to systems of coördinates in uniform movement of translation with regard to one another? What has nature to do with the coordinate systems that we propose and with their motions? Although it may be necessary for our descriptions of nature to employ systems of coördinates that we have selected arbitrarily, the choice should not be limited in any way so far as their state of motion is concerned. (General theory of relativity.) The application of this general theory of relativity was found to be in conflict with a well-known experiment, according to which it appeared that the weight and the inertia of a body depended on the same constants (identity of inert and heavy [p.43] masses). Consider the case of a system of coördinates which is conceived as being in stable rotation relative to a system of inertia in the Newtonian sense. The forces which, relatively to this system, are centrifugal must, in the Newtonian sense, be attributed to inertia. But these centrifugal forces are, like gravitation, proportional to the mass of the bodies. Is it not, then, possible to regard the system of coördinates as at rest, and the centrifugal forces as gravitational? The interpretation seemed obvious, but classical mechanics forbade it.

This slight sketch indicates how a generalized theory of relativity must include the laws of gravitation, and actual pursuit of the conception has justified the hope. But the way was harder than was expected, because it contradicted Euclidian geometry. In other words, the laws according to which material bodies are arranged in space do not exactly agree with the laws of space prescribed by the Euclidian geometry of solids. This is what is meant by the phrase ‘a warp in space.’ The fundamental concepts ‘straight,’ ‘plane,’ etc., accordingly lose their exact meaning in physics.

In the generalized theory of relativity, the doctrine of space and time, kinematics, is no longer one of the absolute foundations of general physics. The geometrical states of bodies and the rates of clocks depend in the first place on their gravitational fields, which again are produced by the material systems concerned.

Thus the new theory of gravitation diverges widely from that of Newton with respect to its basic principle. But in practical application the two agree so closely that, it has been difficult to find cases in which the actual differences could be subjected to observation. As yet only the following have been suggested:

1. The distortion of the oval orbits of planets round the sun (confirmed in the case of the planet Mercury).

2. The deviation of light rays in a gravitational field (confirmed by the English Solar Eclipse expedition).

3. The shifting of spectral lines toward the red end of the spectrum in the case of light coming to us from stars of appreciable mass (not yet confirmed).

The great attraction of the theory is its logical consistency. If any deduction from it should prove untenable, it must be given up. A modification of it seems impossible without destruction of the whole.

No one must think that Newton’s great creation can be overthrown in any real sense by this or by any other theory. His clear and wide ideas will forever retain their significance as the foundation on which our modern conceptions of physics have been built.

A final comment. The description of me and my circumstances in the Times shows an amusing feat of imagination on the part of the writer. By an application of the theory of relativity to the taste of readers, to-day in Germany I am called a German man of science, and in England I am represented as a Swiss Jew. If I come to be regarded as a bête noire, the descriptions will be reversed, and I shall become a Swiss Jew for the Germans and a German man of science for the English!

click for more about this quote and a larger picture • 500px • 800px

(source)

(source)

click for more about this quote and a larger picture • 500px • 800px

(source)

Nature bears long with those who wrong her. She is patient under abuse. But when abuse has gone too far, when the time of reckoning finally comes, she is equally slow to be appeased and to turn away her wrath. (1882) -- Nathaniel Egleston, who was writing then about deforestation, but speaks equally well about the danger of climate change today.

Carl Sagan: In science it often happens that scientists say, 'You know that's a really good argument; my position is mistaken,' and then they would actually change their minds and you never hear that old view from them again. They really do it. It doesn't happen as often as it should, because scientists are human and change is sometimes painful. But it happens every day. I cannot recall the last time something like that happened in politics or religion. (1987) ...(more by Sagan)

Albert Einstein: I used to wonder how it comes about that the electron is negative. Negative-positive—these are perfectly symmetric in physics. There is no reason whatever to prefer one to the other. Then why is the electron negative? I thought about this for a long time and at last all I could think was “It won the fight!” ...(more by Einstein)

Richard Feynman: It is the facts that matter, not the proofs. Physics can progress without the proofs, but we can't go on without the facts ... if the facts are right, then the proofs are a matter of playing around with the algebra correctly. ...(more by Feynman)

Quotations by: • Albert Einstein • Isaac Newton • Lord Kelvin • Charles Darwin • Srinivasa Ramanujan • Carl Sagan • Florence Nightingale • Thomas Edison • Aristotle • Marie Curie • Benjamin Franklin • Winston Churchill • Galileo Galilei • Sigmund Freud • Robert Bunsen • Louis Pasteur • Theodore Roosevelt • Abraham Lincoln • Ronald Reagan • Leonardo DaVinci • Michio Kaku • Karl Popper • Johann Goethe • Robert Oppenheimer • Charles Kettering  ... (more people)

Quotations about: • Atomic  Bomb • Biology • Chemistry • Deforestation • Engineering • Anatomy • Astronomy • Bacteria • Biochemistry • Botany • Conservation • Dinosaur • Environment • Fractal • Genetics • Geology • History of Science • Invention • Jupiter • Knowledge • Love • Mathematics • Measurement • Medicine • Natural Resource • Organic Chemistry • Physics • Physician • Quantum Theory • Research • Science and Art • Teacher • Technology • Universe • Volcano • Virus • Wind Power • Women Scientists • X-Rays • Youth • Zoology  ... (more topics)