| JUNE 16 - BIRTHS | |
| Archie Fairley Carr | |
(source) |
 Born 16
June 1909; died 21 May 1987
American biologist who was recognized as the foremost authority on turtles. He was most noted for his pioneering work in studying sea turtles. He classified 79 species and subspecies of turtles. Extensive work at Tortuguero and Ascension Island earned him the title of "Turtle Man." His work also dispelled the myths and folklore about turtles. From his extensive studies of migratory, nesting, mating, and nutritional habits of turtles he was able to locate the optimal areas for turtles to live and breed. His consistent effort for the conservation of turtles helped to increase their population throughout the world. Carr invented the "five dollar tag" to tag turtles. He published several hundred articles and for the Time Life Books series on natural history of Africa. |
| George Gaylord Simpson | |
(source) |
Born 16
June 1902; died 6 Oct 1984.
U.S. paleontologist known for his contributions to evolutionary theory and to the understanding of intercontinental migrations of animal species in past geological times. Simpson specialized in early fossil mammals, leading expeditions on four continents and discovering in 1953 the 50-million-year old fossil skulls of dawn horses in Colorado. He helped develop the modern biological theory of evolution, drawing on paleontology, genetics, ecology, and natural selection to show that evolution occurs as a result of natural selection operating in response to shifting environmental conditions. He spent most of his career as a paleontologist at the American Museum of Natural History. |
| Barbara McClintock | |
(source) |
Born 16
June 1902; died 3 Sep 1992.
American scientist regarded as one of the most important figures in the history of genetics. In the 1940s and 1950s McClintock's work on the cytogenetics of maize led her to theorize that genes are transposable - they can move around - on and between chromosomes. McClintock drew this inference by observing changing patterns of coloration in maize kernels over generations of controlled crosses. The idea that genes could move did not seem to fit with what was then known about genes, but improved molecular techniques of the late 1970s and early 1980s allowed other scientists to confirm her discovery. She was awarded the 1983 Nobel Prize in Physiology or Medicine, the first American woman to win an unshared Nobel Prize. |
| Georg Wittig | |
(source) |
Born 16
June 1897; died 26 Aug 1987
German chemist whose studies of organic phosphorus compounds won him a share (with Herbert C. Brown) of the Nobel Prize for Chemistry in 1979. In 1953, he discovered how a family of organic compounds called ylides could form the basis of the Wittig reaction, which easily and predictably joins two carbon atoms from different molecules to form a double bond. The Wittig reaction's reliability enabled other chemists to pursue and publish findings on thousands of applications for linking large carbon molecules. The process was used for synthesizing complex compounds such as vitamin A, vitamin D derivatives, steroids, and biological pesticides. Because of the Wittig reaction, such compounds can now routinely be synthesized. |
| Otto Eisenschiml | |
(source) |
Born 16
June 1880; died 7 Dec 1963.
Austrian-American chemist and historian. After obtaining a university degree in Vienna he emigrated to the U.S. (1901). He worked as a chemist with the American Linseed Co. In 1910, with Norman Copthorne, he developed a method of determining the presence of fish oils in vegetable oils, and the method was adopted by the U.S. Dept of Agriculture in 1925. Earlier, he had developed the first one-piece window envelope for the Window Envelope Company. Partly to supply the Window Envelope Company with a special varnish for its envelopes, Eisenschiml established the Scientific Oil Company (now Scientific Chemicals, Inc.) He also wrote over a dozen books on the Civil War; the best known is Why Was Lincoln Murdered? (1937). |
| Edward Davy | |
| Born 16
June 1806; died 26 Jan 1885
English physician, chemist, and inventor. After studying medicine and beginning a career as a chemist, he became interested in telegraphy. He devised the electromagnetic repeater for relaying telegraphic signals (1836) which made wireless telegraphy possible, and invented an electrochemical telegraph (1838). In 1839, he emigrated to Adelaide, South Australia, where he was a farmer and physician. |
|
| Julius Plücker | |
(source) |
Born 16
June 1801; died 22 May 1868.
German mathematician and physicist whose work suggested the far-reaching principle of duality, which states the equivalence of certain related types of theorems. He also discovered that cathode rays (electron rays produced in a vacuum) are diverted from their path by a magnetic field, a principle vital to the development of modern electronic devices, such as television. At first alone and later with the German physicist Johann W. Hittorf, Plücker made many important discoveries in spectroscopy. Before Bunsen and Kirchhoff, he announced that spectral lines were characteristic for each chemical substance and this had value to chemical analysis. In 1862 he pointed out that the same element may exhibit different spectra at different temperatures. |
|
Sitewide search within all Today In Science History pages: Custom Quotations Search - custom search within only our quotations pages: Today in Science History Science Store Click here to browse a selection of Bargain Science and Nature Books |
| JUNE 16 - DEATHS | |
| Sir John Randall | |
 Died
16 June 1984 (born 23 Mar 1905)
English physicist whose critical improvements to the cavity magnetron, the microwave-generating device used in radar, was a major contribution to winning WWII. A magnetron is now commonplace in homes inside the microwave oven. Earlier magnetrons made in the 1920's gave low power output. By Feb 1940, development by Randall with Harry Boot of the small-sized cavity magnetron which generated centimeter wavelengths at much higher power allowed radar to detect smaller objects. In turn, this more compact equipment with a smaller antenna permitted easy mobile installation of high-resolution radar in aircraft. After the war, Randall turned to biophysics, including directing experimental work on DNA structure.« |
|
| Jule Gregory Charney | |
(source) |
Died
16 June 1981 (born 1 Jan 1917)
American meteorologist who, working with John von Neumann, first introduced the electronic computer into weather prediction (1950) and improved understanding of the large-scale circulation of the atmosphere. The entire Oct 1947 issue of the Journal of Meteorology published his Ph.D. dissertation, (UCLA, 1936) Dynamics of long waves in a baroclinic westerly current. It emphasized the influence of "long waves" in the upper atmosphere rather than the existing practice of emphasis on the polar front. It also simplified analysis of perturbations of these waves using mathematically rigorous methods that yielded useful physical interpretation. He helped the U.S. Weather Bureau set up (1954) a numerical weather prediction unit. |
| Wernher von Braun | |
(source) |
Died
16 June 1977 (born 23 Mar 1912)
Wernher Magnus Maximilian von Braun was a German-born American engineer who was one of the most important developers of rockets and their evolution to applications in space exploration. His interest began as a teenager in Germany, and during WW II he led the development of the deadly V–2 ballistic missile for the Nazis (which role remains controversial). After war, he was taken to use his knowledge to produce rockets for the U.S. Army. In 1960, he transferred to the newly formed NASA and became director of Marshall Space Flight Center and chief architect of the Saturn V launch vehicle used to put men on the moon. His contributions include the Explorer satellites; Jupiter, Pershing, Redstone and Saturn rockets, and Skylab.«  Dr.
Space: The Life of Wernher von Braun, by Bob Ward. |
| Sir John Reith | |
(source) |
Died
16 June 1971 (Born in 20 Jul 1889)
(1st Baron) John Charles Walsham Reith was the first Director-General of the British Broadcasting Corporation (1927-38). Reith was often called the "father of the BBC." Although educated as a civil engineer, he was regarded as the dominant influence in British broadcasting. Under his control the technological side of broadcasting rapidly developed, program schedules were enlarged, and a policy of running the radio absolutely free from commercial and political bias was instated and zealously preserved. Largely due to Reith's resistance to political interference with newscasts, the BBC gained a reputation for reliability that endured long after he left the corporation in 1938. He died in Edinburgh |
| Elmer Sperry | |
(source) |
Died
16 June 1930 (born 12 Oct 1860)
American electrical engineer and inventor of the gyrocompass. In the 1890's he made useful inventions in electric mining machinery, and patent electric brake and control system for street- or tramcars. In 1908, he patented the active gyrostabilizer which acted to stop a ship's roll as soon as it started. He patented the first gyrocompass designed expressly for the marine environment in 1910. This "spinning wheel" gyro was a significant improvement over the traditional magnetic compass of the day and changed the course of naval history. The first Sperry gyrocompass was tested at-sea aboard the USS Delaware in 1911 and established Sperry as a world leader in the manufacture of military gyrocompasses for the next 80 years. Elmer
Sperry : Inventor and Engineer, by Thomas Parker Hughes |
| John Ferguson McLennan | |
| Died
16 June 1881 (born 14 Oct 1827)
British lawyer and anthropologist who undertook a vast comparative research of the ceremonies of marriage. His theory of social evolution, in which he first used the termsexogamy (marriage outside the group) and endogamy (marriage within the group), stemmed from his interest in the survival of primitive cultures. He did much to stimulate and guide anthropological research. He developed influential theories on cultural evolution, kinship and the origin of religion. McLennan's pioneering work on totems (as survivals of primitive worship of fetishes, plants, animals and anthropomorphic gods) had a great influence upon contemporary social scientists, including Sigmund Freud. McLennan was influenced strongly by Darwin's theory of evolution. |
|
| Crawford W. Long | |
(source) |
Died
16 June 1878 (born 1 Nov 1815)
Crawford Williamson Long was an American physician who was the first in the U.S. to use ether as anesthetic in surgery. On 30 Mar 1842, practicing in rural Georgia, he first used ether anesthetic while he removed a tumour from a patient's neck. Although he operated more times with ether before 1846, he was apparently unaware of its full significance and did not publish a description of his procedure until 1849. By that time, W.T.G. Morton of Boston had filed a patent for discovery of ether in 1846 and Long would never get much credit or gain from claim to priority. In 1850, he moved to Athens, Georgia, acquiring a large practice and an apothecary shop. There he used ether in obstetrical cases and did much charitable work for the poor. |
| John Snow | |
|
Died
16 June 1878 (born 15 Mar 1813)
English obstetrician who was among the first to use anesthesia, renowned as a pioneer epidemiologist. In On the Mode of Communication of Cholera (1849), Snow suggested that cholera was a contagious disease easily transmitted by contaminated water. The widely-held theory was that diseases are caused by bad air and his idea was ignored. Then, in London's 1854 cholera emergency, he painstakingly correlated individual cholera casualties to the water supply they had used in each case. He thus solved the deadly epidemic by removing a pump handle of the community water pump that he found to be the culprit. Investigation showed raw sewage from a cesspit had contaminated the well.« Cholera,
Chloroform and the Science of Medicine: A Life of John Snow,
by Peter Vinten-Johansen. |
| John Gorrie | |
(source) |
Died
16 June 1855 (born 3 Oct 1803)
American physician and early pioneer in the invention of the artificial manufacture of ice, refrigeration, and air conditioning. While he was a Naval officer stationed at Apalachicola Florida when he needed ice to treat malaria patients with fever, for, he reasoned, people living in cold climates never got malaria. He built a small steam engine to drive a piston in a cylinder immersed in brine. The piston first compressed the air, and then on the second stroke, when the air expanded, it drew heat from the brine. The chilled brine was used to cool air or make ice. He was granted the first U.S. Patent for mechanical refrigeration in 1851. Dr. Gorrie was posthumously honored by Florida, when his statue was placed in Statuary Hall in the U.S. Capitol. |
| JUNE 16 - EVENTS | |
| Life-form patent landmark ruling | |
(source) |
In 1980, the U.S. Supreme Court ruled
that a patent could be issued for a genetically-engineered bacterium in
the case of Diamond vs. Chakrabarty. In a landmark decision, the judges
held five to four that the Patent Office should recognize "any" new and
useful "manufacture" or "composition of matter," and that the fact that
micro-organisms are alive was without legal significance in the related
patent law. Arguments were heard
on 17 Mar 1980, when microbiologist, Ananda Chakrabarty appealed the rejection
of his 1972 patent application for a human-made, genetically engineered
bacterium capable of breaking down crude oil, which no naturally occurring
bacteria could do. Patent No. 4,259,444 was eventually issued
31 Mar 1981.« [Image:
the patented Burkholderia cepacia bacterium; inset:
Chakrabarty] |
| Gas-turbine electric locomotive | |
(source) |
In 1949, the first gas turbine-electric locomotive in the U.S. was publicly
demonstrated
in, Erie, Pa. In 1946, a specific project to develop a gas turbine for
railroad application got under way. After extensive stationary tests at
Schenectady, the turbine was taken to Erie and was installed as the power
plant of a locomotive. Track tests began 15 Nov 1948. The gas-turbine engine
was originally designed for aircraft, in which it gives forward thrust
from the reaction of its exhaust stream. In the locomotive, the power from
the turbine was used to drive a generator supplying electric power to eight
traction motors driving the locomotive wheels. |
| Helicopter | |
(source) |
In 1922, Henry A. Berliner demonstrated the first helicopter prototype
for representatives of the U.S. Bureau of Aeronautics in College Park,
Maryland. Berliner
made this first ever controlled horizontal helicopter flight in a war-surplus
Nieuport 23 fighter with tilting tail rotor, and a short-span upper wing
with 14-ft helicopter blades at the tips. It was powered
with a Bentley 220 hp engine to the front which turned the two counter-rotating
lifting rotors through a series of geared shafts. The two rotors could
tilt slightly in opposite directions to control yaw. Two sets of five 36-in
x 8-in louvers, located below each rotor, opened and closed differentially
to provide roll control by presenting a flat surface, which reacted against
the rotor downwash. |
| IBM | |
(source) |
In 1911, the Computing-Tabulating-Recording Company (CTR) was incorporated,
a predecessor
of IBM (1924). Earlier, in 1890, Dr. Herman Hollerith had constructed
an electromechanical machine using perforated cards for use in the U.S.
census, and in 1896 he founded the Tabulating Machine Co. to construct
sorting machines. In 1911, CTR was the result of the merger
of the Tabulating Company (founded by Hollerith), the Computing Scale Company,
and the International Time Recording Company) |
| Ford | |
(source) |
In 1903, Ford Motor Company, the vehicle manufacturer, was incorporated.
By 1899 Ford had already produced
an operable car that was written up in the Detroit Journals. Ford was described
as a "mechanical engineer." After some false starts, on 16 Jun 1903, with
ten investors plus Ford's patents, knowledge and engine, Henry Ford incorporated
the Ford Motor Company. They signed incorporation papers and sent them
to Michigan's State Capitol in Lansing. Then with only $28,000 they went
out on the limb and made a company that changed 20th century America. The
cars would be built
in a converted wagon factory on Mack Avenue in Detroit. On 20 Jul 1903,
the Ford Motor Co. sold its first car, a Model A, to a Detroit physician. |
| Pepsi-Cola | |
(source) |
In 1903, Pepsi-Cola Co. registered the Pepsi-Cola
trademark with the U.S. Patent Office. Pharmacies at the time were favorite
gathering places. To increase business at his store's soda fountain, pharmacist
Caleb D. Bradham created
a soft drink. In the summer of 1898, he mixed carbonated water, sugar,
vanilla, oils, pepsin, and kola nut extract. Customers at in his pharmacy
in New Bern, N.C., liked the beverage and called it Brad’s Drink. As its
popularity grew, Bradham changed the name to Pepsi-Cola. The name emphasized
the pepsin and kola nut extract it contained for their supposed health
benefits. Pepsin, an enzyme, was thought to aid in digestion, and caffeine,
an alkaloid found in kola nuts, was believed to bestow beneficial energy. |
| Cracker Jack | |
(source) |
In 1893, Cracker Jack was invented by R.W. Rueckheim, a unique popcorn,
peanuts, and molasses confection which he introduced at the World's Columbian
Exposition, Chicago's First World Fair. The company is called F.W. Rueckheim
and Brother. In 1896, Louis Rueckheim , F.W.'s brother and partner, discovers
the process for keeping the molasses-covered popcorn morsels from sticking
together. This secret formula is still in use to this day. In 1912, "A
Prize in Every Box" was introduced with toys inserted into every package.
In 1918, Sailor Jack and his dog, Bingo, first appeared on packages. Sailor
Jack was modeled after F.W. Rueckheim's young grandson, Robert. |
| Roller coaster | |
 |
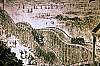
In 1884, the first gravity-powered American roller coaster that was commercially
successful was put in operation at Coney Island, N.Y., the invention of
La Marcus Thompson (patent No. 310,966).
Passengers rode a train on undulating tracks over a wooden structure 600-ft
long. The train started at a height of 50-ft on one end and ran downhill
by gravity until its momentum died. Passengers then left the train and
attendants pushed the car over a switch to a higher level. The passengers
returned to their sideways facing seats and rode back to the original starting
point. Admission on the Thompson Switchback Railway was 5 cents and he
grossed an average of $600 / day. Within 4 yrs he had built about 50 more
across the U.S. and in Europe. |
| Cavendish Laboratory | |
|
In 1874, the Cavendish
Laboratory was opened*
at the University of Cambridge, England. It was built as a teaching
laboratory with a regular course of instruction - a new idea for the time.
Until then, much of experimental physics was conducted as individual work
in essentially private laboratories. Joule and Cavendish,
for example, set up their facilities in their own home, at their own expense.
An early exception was the laboratory at the University of Glasgow established
in the 1840's by William Thompson (later Lord Kelvin). The first Cavendish
Professor (1871-1879) was James Clerk-Maxwell, followed by Lord Rayleigh
(1879-1884), who both much expanded knowledge of physics. The third Cavendish
Professor was J.J. Thomson, discoverer of the electron.« |
|
| Pendulum clock patent | |
(source) |
In 1657, the first pendulum clock was patented
by its inventor, Christiaan Huygens. Although others may have worked in
this field before him, Huygens made major advances in building a practical
clock. He needed time accuracy for his astronomical measurements. |
