 |
The
inventors' paradox
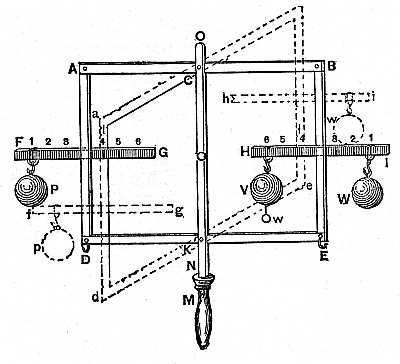
A demonstration
by Dr. Desaguliers in 1719, in regard to the balance of weights at
unequal distances from the center of oscillation, showing that the
weight P balances the weight W at any position on the cross arm H, I,
on the vertical arm B, E, when pivoted to the double-scale beam A, B,
and D, E, in which the resolution of forces is made apparent in a
practical form so often over-looked by the inventors of
perpetual-motion machines.
The cut representing Desaguliers' balance, with his explanation, goes to show how persistently inventors have ignored the geometrical bearing of this problem for nearly two centuries.  Desaguliers'
Demonstration.- A, C, B, E, K, D is a balance in the form of a
parallelogram passing through a slit in the upright piece, N, O,
standing on the pedestal, M, so as to be movable upon the center pins C
and K. To the upright pieces, A, D and B, E, of this balance, are fixed
at right angles the horizontal pieces F, G and H, I. That the equal
weights, P, W, must keep each other in equilibrium is evident; but it
does not at first appear so plainly, that if W be removed to V, being
suuspended at 6, yet it shall still keep P in equilibrium, though the
experiment shows it. Nay, if W be successively moved to any of the
points, 1, 2,3, E, 4, 5, or 6, the equilibrium will be continued; or
if, W hanging at any of those points, P be successively moved to D, or
any of the points of suspension on the crosspiece, F, G, P will at any
of those places make an equilibrium with W. Now, when the weights are
at P and V, if the least weight that is capable to overcome the
friction at the points of suspension C and K be added to V, as w, the weight V will overpower, and
that as much at V as if it was at W. As the lines A, C and K, D, C, B and K, E, always continue of the same length in any position of the machine, the pieces A, D and B, E will always continue parallel to one another and perpendicular to the horizon. However, the whole machine turns upon the points C and K, as appears by bringing the balance to any other position, as a, b, e, d, and, therefore, as the weights applied to any part of the pieces F, G and H, I can only bring down the pieces A, D and B, E perpendicularly, in the same manner as if they were applied to the hooks D and E, or to X and Y, the centers of gravity of A, D and B, E, the force of the weights (if their quantity of matter is equal) will be equal, because their velocities will be their perpendicular ascent or descent, which will always be as the equal lines 4l and 4L, whatever part of the pieces F, G and H, I the weights are applied to. But if to the weight at V be added the little weight, w, those two weights will overpower, because in this case the momentum is made up of the sum of V and w multiplied by the common velocity 4L. Hence it follows, that it is not the distance, C6, multiplied into the weight, V, which makes its momentum, but its perpendicular velocity, L4, multiplied into its mass. This is still further evident by taking out the pin at K; for then the weight, P, will overbalance the other weight at V, because then their perpendicular ascent and descent will not be equal. This "paradox" is illustrated in No. 10, first volume of Mechanical Movements, inviting inquiry by students, a model of which has been exhibited to many doubting amateurs by the author. (Subsection 914, from p.364-5) 
 |